 This post is working towards a paper I will call Logic Driven Physics. At the moment, I believe that I am the only person in the world writing this story of how the science of the Stoics can be reverse engineered to provide a new, alternative take on physics, logic, and mathematics.
This post is working towards a paper I will call Logic Driven Physics. At the moment, I believe that I am the only person in the world writing this story of how the science of the Stoics can be reverse engineered to provide a new, alternative take on physics, logic, and mathematics.
In this post, I consider physical reality as a system. I take a leaf out of system science where there is not one paradigm for understanding a system but two. I argue that the foundations of science, including physics and mathematics, must be bilateral. System science demands two takes on reality. One take is diachronic in nature, the other synchronic. In system science, the diachronic side employs ordinary calculus and studies time series whilst the synchronic side employs the operational calculus pioneered by Heaviside and sees its reality as having a “holographic” flavour nowadays in Laplace and Fourier transforms.

Heaviside pioneered
Operational Calculus
I sometimes like informally to refer to this dichotomy between the diachronic and synchronic as expressing “left side” and “right side” rationality respectively. Thus, one can imagine this bilateral architecture as two diametrically opposed but complementary hemispheres of a metaphorical epistemological brain.
Aristotle was the first to remark on the epistemological dichotomy of knowledge. He placed the traditional science on one side charactering them as all studying objects that have a determined genus. On the other side he placed an entirely different kind of science that was characterised by studying entities with completely undetermined genus. The latter science became known as metaphysics which, to Aristotle, was the science of Being, pure otology. Writing about metaphysics, Kant once bemoaned:
It seems almost ridiculous, while every other science is continually advancing, that in this, which pretends to be Wisdom incarnate, for whose oracle every one inquires, we should constantly move round the same spot, without gaining a single step. (Kant, 1781)
The same thing can be said in modern times with the plight of metaphysics now in disarray where metaphysics is often demeaned, even ridiculed by many scientists. The objective of this post is to correct the slide of metaphysics into scientific oblivion. My first step is to demystify the subject by citing the non-diachronic approach of Operational Calculus as an example of what I call weak metaphysics. According to my formulation, strong metaphysics must be strongly synchronous. This demands that all pertinent players must be simultaneously present in any whole. The Operational Calculus can represent a simple system as a whole. That is its speciality. However, these kinds of systems are made up of objects only. There are no subjects present in the synchrony. Strong metaphysics, as we shall see, demands that not only must all objects be present but also the subject.
A characteristic of weak metaphysics is that the relationship between the diachronic and the synchronic is deterministic. For example, for the relationship between calculus (diachronic) and the operational calculus (synchronic) can be actually calculated exactly by Laplace transforms. In strong metaphysics, an exact calculation is impossible—such relationships can only be known in terms of dispositions, not coordinates and determined quantities.
Despite the lack of individual subject, weak metaphysics such as Operational calculus does illustrate a number of important characteristics of a strongly metaphysical right side science. Of crucial importance is Aristotle’s original characterisation of metaphysics. Unlike the world of calculus, the objects that make up the world of Operational Calculus all have undetermined genus with respect to each other. In the diachronic domain, a simple system is made up of a conglomerate of entities of differing genus, such as inputs, outputs, and system behaviours. In the synchronic domain all such categorical distinctions vanish: all entities are represented in exactly the same way as functions of a complex variable. Using a term borrowed from Computer Science, one can say that all the entities in the synchronic domain are first class. Aristotle’s undetermined genus characterisation becomes a demand that all entities in the system must be first class. Operational Calculus also demonstrates another common characteristic of right side methodology. The first class entities form an algebra. All of the complicated operations in the diachronic domain can be expressed in this algebra providing great simplification.
Another weak metaphysics example is Geometric Algebra (GA). which provides an operational alternative to the traditional matrix and tensor dominated approach of linear algebra. In GA all entities are first class where tensors, matrices and vectors give way to the same kind of entity. Everything in GA becomes a geometric entity. Like in OC, the geometric entities form a simple algebra where, in the case of GA, the role of Grassmann’s geometric product is paramount. The work of Hongbo Li highlights this key aspect of this operational methodology (Li, 2008). Li applies the conformal aspects of GA methodology to provide remarkably simple automated proofs of geometric theorems. A key construct in his algorithms is to privilege as much as possible multiplicative operations at the expense of the additive. To Li, more additive operations mean more algebraic clutter and leads to what he calls mid-term-swell. On the other hand, more of the multiplicative means the retention of geometric meaning and results in great simplification. Li clearly demonstrates how automated proofs and geometric computation in general can be greatly simplified using his approach. With more traditional linear algebra and brute force Clifford algebras the resulting mid-term-swell can be so enormous that solutions become, at best, purely notional. Another key term emerging from Li’s work is the purely multiplicative polynomial, the monomial. The monomial expresses pure geometric semantics based on multiplication, free of additive algebraic clutter. In many cases, Li’s methodology resulted in expressing geometric concepts that distilled down to monomials leading to spectacularly simple solutions free of the dreaded mid-term-swell phenomenon that afflicts non-operational methodology. As will be seen further on, the monomial construct will turn out to be of fundamental importance in this project.
In passing, one should note that the modern formulators of GA such as David Hestenes as well as Li consistently claim GA to be the universal algebra of physics and mathematics (Hestenes, 1988). I concur with this appreciation of GA with the proviso of introducing a number of important ingredients reported in this post.
There is one other example of a weak metaphysics methodology that I will be examining in more detail further on. It might seem surprising that I put forward Gödel’s work on the Completeness Theorem and Incompleteness Theorems as such an example. His work is important for this project as it brings into play the logical dimension of metaphysics. moreover, the dichotomy between what is true and, more fundamentally, what is the truth. Of great significance is the fact that Gödel’s work is not mere metaphysical speculation as it takes place in the full glare of an ingenious mathematical formalism. More of that later.
Contribution of the Stoics
Operational Calculus and Geometric Algebra provide clear examples of operational methodology. They illustrate an important aspect of metaphysics in the sense of the first classness of the fundamental entities. However, they do not embrace the most fundamental aspect of including not just a science of object nut also a science of subject. In order to start getting a grasp of what is meant, I turn back to the philosophical terrain of Hellenistic times. The bilateral perspective that I am trying to explain, can be seen in the schism between the Epicurean and Stoic schools of thought of that time.
The diachronic left side take was advocated by the Epicureans. The Epicureans were atomists, and believed in a materialist, deterministic world view that is not incompatible with the view of traditional modern science. The exception to absolute determinism was the famous Epicurean Swerve construct whereby, according to the Epicurean doctrine, every now and then atoms would imperceptibly deviate from a strictly deterministic trajectory. In this way, the unstructured primordial universe somehow micro-swerved to evolve to the state it is today. In the broad sweep of the history of ideas, I see the Epicureans and their atomist forebears as early exponents of the left side, diachronic take on reality.
Of central interest in this post are the much less understood early exponents of right side non-diachronic reality. Here, I am talking about the implacable foes of the Epicureans, the Stoics The alternative right side approach, exemplified by the Stoics, concentrates on studying the world in between the a priori and the a posteriori, the world that exists now relative to the organism in question. For the Stoics, only corporeal bodies with extension exist. Only what exists can act upon and be acted upon. Objective reality is sandwiched between the a priori and the a posteriori. To the Stoics, things in the past or in the future do not exist. It is only what exists now, relative to the organism in question. Heroes of the Now, the Stoics had no fear of anything in the past or the future; as such, things simply do not exist.
As Hahm remarks “For half a millennium Stoicism was very likely the most widely accepted worldview in the Western world.” (Hahm, 1977) However, it was the world view of the diametrically opposed Epicureans that best corresponds to the present day analytic, diachronic world view of our time, not that of the Stoics. Moreover, Stoic physics, according to my characterisation, is not physics as the moderns understand it but metaphysics. As such, their perspective on reality should be operational. This is indeed the case as Stoic physics ticks all the boxes in providing an operational perspective on reality. First of all, Stoic reality is articulated in terms of first class entities according to the mantra: everything that exists is a material body. For the Stoics, the property of an entity was also an entity in its own right thus guaranteeing that entities are first class. Thus in Stoic physics, properties are also material bodies. As for the entities forming an algebra, at least the Stoics identified the letters of the algebra in borrowing the four primordial letter alphabet of Empedocles. This necessarily leads to acceptance of the ancient four-element theory of matter where each primordial element corresponds to one of Empedocles’ four “root” letters.
The Stoics also borrowed from Heraclitus. Heraclitus saw everything in terms of oppositions. Each of the four elements expressed a primordial tension between opposite poles of an opposition. These elements were called Air, Water, Earth, and Fire. Air represented an expansive tension. Water a contractive tension corresponding to the images evoked by such naming. Earth would (or should, according to me) have been seen as an unsigned tension between two different extensions. Earth would have been seen as an unsigned tension between two different (but indistinguishable) singularities. Physical reality for Heraclitus could thus be interpreted as the interplay of these four primordial tensions. Heraclitus saw these primordial tensions as four instances of one single even more primordial tension called pneuma. Thus, the four element theory became a five element theory of sorts.
Category Theory and the Five Morphisms
To modern eyes, the ancient four element theory might seem like abstract nonsense. However there is a branch of mathematics that sometimes actually prides itself on its “Abstract Nonsense,” viz. Category Theory. Category Theory, despite being encased in a diachronic axiomatic framework, also reveals operational aspirations. Its first classness is expressed in the mantra: Everything is a morphism. Morphisms can be represented by arrows and so Category Theory sees its reality in terms of dyads, not monads as does straight pure and simple Set Theory. Category Theory rediscovers Heraclitus’s four kinds of tension in terms of four distinct kinds of morphism. Instead of Air, Water, Earth, and Fire, Category comes up with four kinds of morphism, the epimorphism, monomorphism, bimorphism, and isomorphism. In Set Theory these morphisms become functions. For functions, there is no difference between bimorphisms and isomorphisms. Note also the “expansive” nature of an epi, the “contractive” nature of a mono, and that the inverse of a bi or iso is a bi or iso, much as Heraclitus would have expected.
The vocation of Category Theory is to study mathematical structures which are common to all mathematics. Thus one could say that that these four kinds are morphisms constitute the stuff that mathematics is “made of.” Note also that there is an even more primordial morphism in Category Theory than these four, the natural transformation. Saunders Mac Lane, cofounder of Category Theory, once stated that he invented Category Theory in order to study natural transformations. Natural transformations take up the fifth spot in a “five element theory of mathematics.”
Stoic Logic
The Stoics embraced Heraclitus’s theory of the five elements and the primordial tensions they convey and incorporated it as the basis for their physics. The Stoics claimed that their philosophical system included physics together with logic and ethics to make up a harmonious whole. However, as de Lacy back in 1945 commented:
One of the many paradoxes associated with Stoicism is the puzzling circumstance that although the Stoics themselves claimed that their philosophy was a perfectly unified whole – so well unified indeed that its various parts could not be separated from one another, and the change of a single item would disrupt the whole system, yet the opponents of Stoicism, even in ancient times, regarded the Stoic philosophy as a mass of inconsistent and incompatible elements. Since much of our information about Stoicism comes from hostile sources, it is much easier for the modern investigator to find the inconsistencies of Stoicism than its unity. In recent years there have been a number of studies attempting to find the unifying element, but the problem is by no means solved. (de Lacy, 1945)
The situation hasn’t advanced much since then. In this post based on previous work, I provide the unifying element for the Stoic system. For the moment, I will simply point out the structural similarities between Stoic physics and Stoic logic.
Stoic logic in its entirety covered a vast range of subject matter ranging from rhetoric to dialectics including many subjects that would not be regarded as logic from a modern perspective. However, for the purposes of this post we need only consider the core logical system. For the Stoics, rational reality was subject to the logical principles of the Logos L. The Stoic interpretation of the Logos L was in the form of their system Ls based on the five indemonstrables, considered in detail later. A simplistic interpretation of Stoic Logic Ls is to see it as the first historical example of the propositional calculus. In other words it expresses the zero order logic of particulars. In later work, I intend to show further on that Ls can be thought of as a first order logic with powerful spacetime-like geometric semantics Gs.
However, for the moment we must be content with a cursory description of how each of the five indemonstrables map to the corresponding element of the Stoic-Heraclitus physics system Ps.Thus, the question is: how does the Stoic system unite physics with logic? More precisely, how does Stoic logic Ls based on the five indemonstrables relate to the Stoic five element theory of substance Ps? The relationship Ls Ps has already been reported from several different perspectives in previous papers. The essence of the relationship is illustrated in Figure 1.
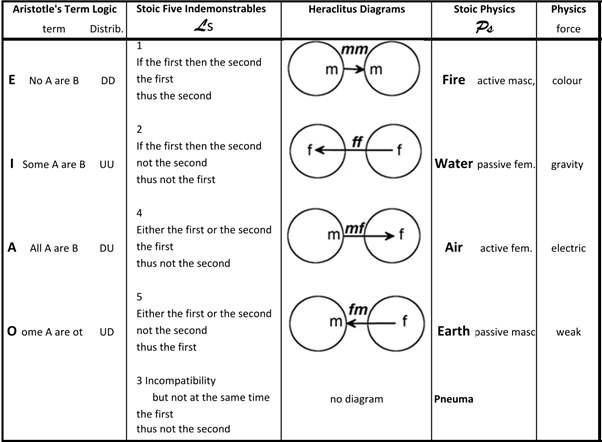
Figure 1 Illustrating the Stoics relationship Ls Ps
and the corresponding Heraclitus diagrams.
Stoic physics adopted the four element system of Empedocoles, including the gender typing. The gender construct is explained in my previous works and will be further explained further on in this work. I technically refer to it is ontological gender. Gender is the key to understanding how all of this fits together. There is a learning curve for appreciating the full extent and subtleties of the gender construct the most subtle of all distinctions. For the moment, think of the masculine as expressing pure form. The purest and most primordial expression of form is the singularity. Expressed linguistically, the masculine is pure “is-a.” On the other side of the gender divide is the feminine which, in isolation, can be thought of as pure formless extension. Linguistically, the feminine is pure “has-a.” The gender calculus (yes it does form a calculus) expresses the dialects of the is-a, and has-relationship. As I said, this is the most subtle of all distinction. It is also the most fundamental.
To be expanded upon….
References
Kant, I., 1781. The Critique of Pure Reason. s.l.:The Project Gutenberg EBook: http://www.gutenberg.org/files/4280/4280-h/4280-h.htm.
Moore, D. J. H., 2012. The First Science and the Generic Code. Parmenidean Press. 450 Pages
Moore, D. J. H., 2013a. Now Machines
Moore, D. J. H., 2013b The Whole Thing is a (Now) Number
Moore, D. J. H., 2013d. Logic Driven Physics: How Nature’s genetic code predicts the Standard Model.
Moore, D. J. H., 2013. The Universal Geometric Algebra of Nature: Realising Leibniz’s Dream
Moore, D. J. H., 2013. Generic Model versus Standard Model Interactive Database. [Online Database Application]