This section is about multiplication. In the large sense, multiplication brings two things together to make a third. In the case of numbers, this leads to simple arithmetic. In the case of two inebriated men at a bar, it can lead to a bar room brawl. The ancients, both in the West and the East, were interested in bringing two principles together, one masculine and one feminine. The multiplication of these two principles created the Cosmos. We will visit the ontological and epistemological roles of gender later. For the moment, we are interested in multiplying together two different ways of thinking, two different takes on reality. In mathematics, there are so many different kinds of multiplication that it can be very overwhelming. We are particularly interested in the role of multiplication in geometry. There is one kind of geometry that is pertinent.. It is called Geometric Algebra (GA). We will consider it in more detail in other sections of our work. GA only has one fundamental product called the geometric product and is closely intertwined with quadratic forms. In this section, we avoid any technicalities, and our algebraic product does not explicitly lead to a quadratic. It leads to another kind of energy powerhouse, the brain. The brain considered is the epistemological brain. This brain is constructed by the product of two different kinds of rationality. We like the product idea so much; we play God and apply the operation to itself. This section is a prelude to things to come.
We have been repeating many times the mantra that there are two takes on reality. From an epistemological viewpoint, this can be seen as two kinds of knowledge, knowledge conditioned by the contingent and knowledge conditioned by the demands of pure reason. We gloss over all of the nuances involved and simply refer to them as conditional and unconditional knowledge. Conditional knowledge corresponds to all of our traditional sciences, including axiomatic mathematics. The big question lies on the unconditional side of knowledge. The only science possible for this kind of knowledge is Aristotle’s First Philosophy, what we will call the First Science. The kinds of thinking involved in these two forms of knowledge, we refer to as left side and right side knowledge, the inference being that the fundamental epistemological dichotomy is mirrored in the architecture of mind, and correspondingly of its implementation as brain.
One common approach to a dichotomy is to interpret it in the thesis-antithesis format leading to some kind of synthesis, which is supposed to resolve the inherent opposition. Some might even claim that this constitutes dialectics. Semiotics offers an alternative approach. Rather than attempt to explain how Nature or Mind might function sequentially as a temporal or logical process, the emphasis is placed on the geometric spatial structure. We concentrate on the shape of knowledge and the corresponding shape of Mind. Appealing to poetic license, we interpret the corresponding structure as the epistemological mind. We may also employ other terms that help us to understand the notion, such as the semiotic brain, and sometimes the metaphorical brain.
The Two Hemispheres
Initially, this metaphorical brain architecture is characterised by a great split down the middle, dividing it into a left and a right hemisphere. This structure carves up scientific knowledge into two camps. Traditional scientific knowledge, and its characteristic way of thinking, is the affair of the left hemisphere. On the other hand, the mysterious yet to be understood, holistic, unifying science, and its way of thinking, belong to the right hemisphere.
The left-right dichotomy expresses the first fundamental principle of consciousness. There can be no consciousness without something to be conscious about. The fundamental dichotomy at play here is between the object of consciousness and the consciousness of subject. Without any hesitation, we place the object on the left and the subject on the right side of the two hemisphere epistemological brain. What we have here is a basic formula that conscious being can be expressed as am opposition between the subject and its world as a conglomerate of objects. it can also be thought of as the “sum” of subject and objects.
Thus
Being = objects + subject (1a)
This simple formula illustrates the left side view of the traditional sciences: any being, as a whole, is nothing more than the sum of the parts. The subject is the organism as a whole, and the objects are the parts. Set Theory in mathematics is a good example. From a Set Theoretic perspective, the predominant mathematical entity, the subject, is the set. Sets are constituted of objects called elements. Of course, the elements themselves can possibly be considered as sets in their own right, just as the sets can themselves be considered as elements of other sets. Bertrand Russel considered this kind of hierarchy of entities in terms of his Theory of Types. According to the theory, a set was of a different type to the elements it contained. A set of sets was thus of a different type to a set, and so on. The main claim to fame of Russell’s Theory of Types is that it provides a simple way of avoiding logical paradoxes such as Russell’s Barber Paradox. However, this is of little interest to our project.
The Opposition of Generic Being
The right side view interprets the relationship as an opposition between two contraries. The opposition can be intuitively expressed in the form:
Being = {objects , subject } (1b)
Whilst the left side approach deals with the mereological sum of the two sides of the opposition, the right side approach treats the opposition as a fundamental dichotomy. The dichotomy is not an absolute dichotomy as what is subject and what is object depends on context.
Just as in the left side perspective, subject and object are of different type. However, in the right side perspective there is no hierarchy of types. The types don’t nest as do Russell’s type system they combine geometrically. In this respect, the right side expression (1b) is allows a geometrical interpretation. The objects are on one side of the dividing line and the subject is on the other. Which side is which? We adopt the convention that the objects are on the left side and the subject on the right. There is nothing fundamental about this convention. Handedness is determined relative to each individual. However, like all convention, once adopted, to avoid all future controversy and paradoxes, the convention should be adhered to, at least as for the individual concerned.
The opposition expressed in (1b) leads to cognitively dividing objects from subject in terms of a geometric opposition between a left and a right side typing of entities. The entities on either side of the oppositions are generic entities. The notion of left side and right side are also generic notions. At the level of individuals, what is right side for one individual may be left side for another.
Further on in this work, we will replace that object-subject dichotomy with a more fundamental and more generic concept, but that requires an understanding of ontological gender. For the moment, the object-subject dichotomy will suffice. The subject and its kingdom of objects make up a whole. This construct is truly universal as it applies anywhere and everywhere.
Sidenote
Many thinkers make the mistake of confusing the general with the universal. The general is an abstract construct and is limited to a closed, conditioned reality. Within its confines, a general law applies to everything. By contrast, the universal is not based on abstraction but is a generic construct. The universal does not apply to everything in some confine, as does the general. The universal, as a generic construct, is free of confines. It is an open system construct. As such, it applies anywhere. In brief, the general applies to everything (within a confine), whilst the universal applies everywhere (but not to everything. From a generic point of view, ‘everything’ is an abstraction that does not even exist).
To be pedantic and more strictly correct, the reference to ‘everywhere’ should always be read as a reference to ‘anywhere’.
The two “parts” in expression (1b) form integral moments of a unified whole. They are inseparable, as one is needed to determine the other. The expression possesses what C. S. Peirce called “vagueness.” In fact there is nothing more vague than this simple expression. The expression literally applies to anywhere you can think of. Wherever the consciousness, any consciousness, directs itself, expression (0) jumps to the fore. Peirce remarked that vagueness should be a focus for formalisation. How do we formalise such a construct so reeking of vagueness?
The vagueness comes about due to the highly undetermined nature of the two entities involved. Essentially, consciousness demands the absolute separation of the object of consciousness from the agent of consciousness. It remains that the object of consciousness is so undetermined that it drowns in Peirce’s sea of vagueness. One must agree that the validity of the expression is inescapable. The concept expressed is absolutely universal as the object of consciousness can be literally anything. On the scale of vagueness, to be conscious of anything would be hard to beat. In order to reduce the level of vagueness, the natural direction would be move from the consciousness of anything to at least the consciousness of something.
We are thus led to two expressions of consciousness, one where the object is anything, and the second where the object is something. Thinking about this can make the head start to spin, but it’s not that complicated. The something referred to here can be anything, but it is not. It is more determined than the allusive anything it is something. The two things are different, so are the two subjects for that matter. The two kinds of Being are also different. However, both expressions must be valid in the same moment. Each of the two expressions determines an opposition. The whole secret of the underlying right side formal system involves oppositions and the oppositions of oppositions. This is what dialectical thinking is all about. Left side thinking is analytical and is expressed rhetorically in order to convince, Right side thinking is dialectical and based on oppositions in order to understand. The question now is to understand how the dialectical notion of two oppositions opposed to each other.
Aristotle provided the germ of the answer but gave few details. He proposed a new science that was different to all others. Traditional sciences all deal with a determined genus of a thing that could be decomposed into species of things and particulars. He proposed a science of a thing that had no determined genus whatsoever. The science became known as metaphysics. Developing such a science has proved so allusive that no progress has ever been made. A science of a thing, totally lacking in genus, Here we see Peirce’s ‘vagueness’ appearing in a new light. According to Aristotle, metaphysics is the science of an entity so vague that it is totally devoid of genus. The study of such an entity was to study Being itself, the science of pure ontology. In Metaphysics, Aristotle grappled with this mysterious entity-without-genus. All of the entities that the traditional sciences study fall under the umbrella of some kind of genus. Aristotle eventually settled for naming this mysterious entity of study for metaphysics in a particular way. He called the object of study for this first of the sciences, the study of being qua being. The exact meaning of this term, being qua being, has been a subject of constant debate over the millennia. Some say that ontology should be simply the study of being, with the term being ‘qua being’ taken as unnecessary.
To avoid sliding into a long interminable debate, we simply present our interpretation as follows. The entity of study, notably pure being, has none other than itself for its genus. Thus being is both an entity and a genus. The genus itself is an entity in its own right. There are thus two entities in play here. The first entity is an entity that has a genus. The second entity is that genus. Unlike the ordinary entities of the traditional science, the entity and its genus are not separable, nor even distinguishable from each other. They from two modes of a common unity.
The unity of a determined entity with its less determined counterpart has long been interpreted from a religious perspective as the unity of the individual with his god. A most obvious example is the non-dualist doctrine of Hindu Advaita philosophy. There the individual. soul is the ātman and the cosmic soul is Braham. They two are different but non-dual. The entity becomes indistinguishable from its genus.
However, such lofty theological matters don’t immediately concern us here. All the same, it is always interesting when one can imagine God in one’s mathematics. Of course, only right side mathematics has that vocation.
In both cases, an opposition between subject and object is involved. A fundamental principle at play is that subject and object are themselves different. In this way, the principle of being is inseparable from the principle of consciousness. Both principles demand a separation of subject from its other. We don’t delve into whether this difference is the result of a conscious effort of a knower or a characteristic of the known. Whether Mind moulds the world or the world moulds Mind, is a question we want to avoid, rather than attempt to answer in one way or the other.
Accordingly, we can consider that the terms ‘being’ and ‘consciousness of being’ can be interchanged. Similarly, the terms ‘object’ and ‘subject’ can be interchanged with the terms ‘consciousness of object’ and ‘consciousness of subject.’
The Opposition of Individual Being
We can start the ball rolling by saying that there are two forms for expressing being as an opposition between subject and object. We represent the first opposition geometrically as a geometric left-right opposition in (1b). This expression is valid for any being whatsoever. It involves the minimal aspect of consciousness of Self or Subject and the consciousness of what is not subject, the object part of the equation. This expression is the universal principle of consciousness. That is why we have referred to it as generic. This form of consciousness has a very high degree of “vagueness” about it, to use Peirce’s term.
Consciousness Incompatibility Principle
In addition to the requirement that consciousness demands the difference between subject and subject, there is also the matter of attention. The fundamental principle at play here is that only one pole of the object-subject can be the centre of attention at the same time. We state this as the Consciousness Incompatibility Principle. As we shall see later, when we reinterpret all of this in the context of ontological gender, the inability principle plays a dominant role in the overall structural integrity of organisms, be they animate or even inanimate.
The next form of being applies, not to universal, generic being, but to individual being. We geometrically represent this opposition as a front-back polarity and express it algebraically as
where the ‘subjects’ term is at the front and the ‘object’ term is at the back of the front-back geometric representation of this opposition.
What now interests us is that Aristotle’s qua functor can be interpreted algebraically. We will interpret the qua operator as a kind of semiotic product. In this respect, substituting the individual and generic forms from the above two expressions we get that
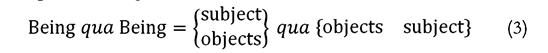Interpreting Aristotle’s ‘qua’ operator as an ‘as’ operation, we get the two by two tensor:
In Figure 2, the four-element tensor is interpreted as the four quarters of our epistemological brain. The basic requirement is that the organism be conscious of its Self and the Self of others. As the diagram illustrates, there are four possibilities. All four possibilities are of equal value. All four are present in consciousness and provide the common ground.
Each of the four regions of this epistemological brain has been categories for its speciality. The science of consciousness divides into four components, as does the epistemological brain that it must study. We have labelled the left frontal lobe as Cognition, the science of studying subjects as object. Cognitive science, seen in this perspective, becomes a traditional left side science. This is the realm that Hegel would refer to as the “empirical Ego.” Cognitive science is the study of the empirical self. The right frontal lobe of our epistemological brain corresponds to the science of Consciousness pure. Hegel would describe this as the realm of the true Ego. This science must be an integral part of right side science. Up until now, right side science, the Frist Science, has not seen the light of day. The task of this work is to make a significant contribution in this regard. In its purest form, this First Science has no determined objects whatsoever. It is a pure science of Subject, a pure science of the conscious Self.
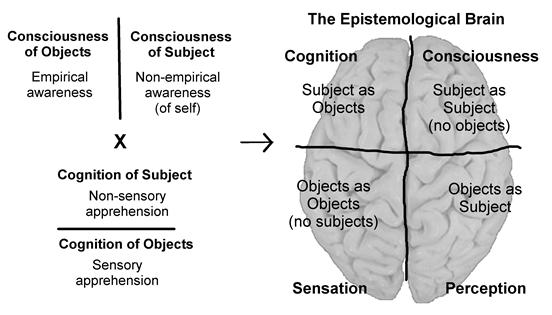
Figure 2 Superimposing via an informal “semiotic product” the two fundamental dichotomies of knowledge leads to an epistemological square. Only right side science is aware of the full significance of this opposition of oppositions and so has the potential for explaining consciousness.
We have categorised the left back area of the epistemological as Sensation. In this region, there are no determined subjects whatsoever, nothing but pure objects, a Buddhist paradise. This is a realm of unhindered sensual objects devoid of any determined subject to sense them. This was a realm explored by David Hume. In this realm, there is no determined knowledge or even direct reference to the Self. The Self appears as a bundle of “lively” sensations. The science of Sensation was touched upon by Hume where he described a world of pure sensations autonomously growing into rational forms. This must be a left side science but of a distinctly different kind than the traditional Western sciences. As will be explained later, such a science will be free of any traditional logic and totally free of abstraction.
On the other right hand back side, we see the realm of perceptions. A science of perceptions must form an integral part of right side science. The ancient Stoics seemed to have had a lot to say about such a science.
…
In constructing this semiotic square, our approach has been highly informal and lacking in any kind of rigour. However, we do end up with an embryonic cognitive form of mind that is not totally ridiculous. Also we have touched on something that will turn out to be very fundamental, an algebraic notion of product, albeit devoid of any mathematical precision. In later development and in the appendices, we will relate this product to the geometric product of the geometry pioneered by the mathematicians Grassmann, Hamilton, and Clifford of the nineteenth century. Can this qualitative, informal approach of semiotics eventually reach maturity and match up with a new kind of geometric algebra based on geometric products? We have a long road to hoe, but that is one of the objectives of this work.