
In any ground breaking project there is a polemical streak and this work is no exception. Topics covered in this blog have raged across the axis of traditional left side science and our proposed right side science. The arena for this epic tussle has been the nature and structure of scientific knowledge. What we have failed to do is clarify exactly what we mean by scientific knowledge. We have argued that there is another kind of scientific knowledge than left side conventional science. This was the right side science. Now we must ask the question as to whether there are any other kinds of knowledge, knowledge that escapes the scientific tag. Embarrassingly, there is another axis of knowledge that is dramatically distinct from the scientific. In this blog, we have ignored this other axis, an axis of equal importance as the left-right science axis.
To begin with, our topic here is universal knowledge, knowledge that includes scientific knowledge as a special case. Universal knowledge is composed of two, and only two, fundamental ingredients. These ingredients are semantics and logic, in the large sense. In order to understand the universal shape of knowledge, one must understand that there are two orders of logic and two orders of semantics: both have a first and a second order form. The notion of first and second order logic is a quite familiar to present day logic, and has been even formalised from an axiomatic perspective. However, this is not the case for semantics. Even the very prevailing notion of semantics is hazy, let alone any notion of first and second order semantics. We must rectify that situation as we proceed.
Attempting to explain the shape of knowledge can take up reams and reams of pages and still not get anywhere very fast. Our best recourse is simply to illustrate the shape of knowledge with the semantic square. As usual, everything finds its place and we get the fit shown below.
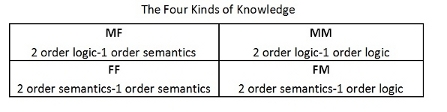
Semiotic square of the four kinds of knowledge
From the diagram we identify logic with the masculine gender and semantics with the feminine. As we have seen, the pure feminine F typed entity has extent but no presence. On the other hand, the pure masculine M typed entity enjoys presence (it is presence) but has no extent. Logic plays in the masculine register and so becomes the logic of presence. The masculine becomes the ultimate determiner of what is and what is not. Semantic plays in the feminine register involving the interplay of that which can claim some substantiality. The minimal requirement for substantiality is extent. The pure feminine has extent but no presence.
Now we come to the question of scientific knowledge. We start with a rough-hewn definition of science in the context of the semiotic square . The parts of the square that qualify as science are the boxes where both M and F are present. M provides the logic and F provides stuff with extent. Science thus fits into the slot of being the “logic of stuff”. This would be the MF version corresponding to traditional left side science. Reversing the order, we get the FM science corresponding to the “stuff of logic.” This corresponds to the right side science that we have been developing. One could surreptitiously slide in the comment that the MF science studies dead stuff whilst the FM science studies living stuff.
Note that we are using the semiotic square as our compass in our attempt to avoid Kant’s curse of the “fine spun argument.” Keep in mind that one does not need to write a doctoral dissertation each time one consults a compass.
Thus, it appears that the main dialectical opposition of this blog has raged along the MF-FM diagonal of the semiotic square. There we find two kinds of science, the traditional left side and the right side science that we are promoting. The semiotic square nicely characterises these two kinds of science. Left side science is based on the paradigm of second order logic and first order semantics. In other words, all the traditional science, including mathematics are based on abstraction provided by a second order logic and the shallow first order semantics. On the other hand there is the generic, and universal oriented right side paradigm, which is totally devoid of abstraction and its higher order generalisations. To remove abstraction from the pudding, the paradigm only allows first order logic. Where it shines, is that it can handle non-trivial second order semantics.
It appears that if you want a science with non-trivial semantics, you have to throw away abstraction and its higher order logic. Vice versa, if you want the generalisation power of abstraction, you have to throw away higher order semantics and use the rather trivial default version based on first order semantics.
Just before going on to explain what is meant by these different orders of logic and semantics, we cast one more glance at the semiotic square of knowledge. Apparently, scientific knowledge works along the MF-FM diagonal of the square. This leaves two other kinds of knowledge left out of our science equation. The other diagonal consists of FF and MM knowledge. This is a topic that we will have to come back to later. For the moment, whatever this kind of knowledge may involve, we will refrain from characterising as “non-scientific.” Rather, we will call these potential science, the subtle sciences. Such sciences have a distinctly Eastern flavour. We shall briefly discuss these subtle sciences later.
Our immediate task is to clarify what is meant by first and second order logic and semantics.
We start with first order logic. From a traditional left side perspective, first order logic comes down to the logic of propositions, the propositional calculus. The propositional calculus involves well-formed formula, called propositions. Each proposition has a truth value of either true or false and is made up logical conjunctions, disjunctions, and negations. In brief, propositions are mathematical logical expressions made up of abstract symbols combined with AND, OR and NOT primitives.
Second order logic is an extension of the propositional calculus and is called the predicate calculus, In addition to the propositional calculus structure, the predicate calculus allows the abstract symbols to be treated as variables with values ranging over sets. Each variable x can take on a range of value restricted to a particular set of values A. This simple construct provides the necessary equipment for abstract logical reasoning. The reasoning is formalised by the addition of two logical primitives called universal and existential operators. The so called universal operator is used to mean that a predicate is valid “for all x,” The existential operator means that “there exists an x” for the logical expression to be true.
Second order logic is the basic construct that enables abstract reasoning. An essential characteristic of abstract reasoning is that the objects of reason are not required to exist. Whether something exists or does not exist may be true or false, depending on the assumptions. The reasoning is based on generalisations and, despite the “universal quantifier” terminology, has no concept of universals. The universals belong to right side science.
Side Note
Generalisations and general laws apply to everything in a closed world. For example, the Second Law of Thermodynamics is a general law and so applies to everything in a closed system. The law states that everything in in the confines of such a system drifts to a state of maximum entropy, that is to say, to a state of thermic death. One can say that general laws apply to everything but not everywhere. They only apply to within the closed system. The general law is only valid in the confines of a sealed bottle. The bottle may be made of glass and contain a mixture of gases. Glass is a favourite material for making sealed systems for the left side sciences. Another favourite material for building a closed system is axioms. Axioms make very fine watertight bottles and ensure that everything enclosed within is sure to be headed towards thermic death.
On the other hand, universal laws apply everywhere but not to everything. Instead of applying to the closed system, the universal law applies to the open system, the system that, instead of living in a bottle, lives within itself. Instead of drifting to thermic death, the universal system will tend to proliferate and diversify, producing life.
In addition to second order logic, left side science must have recourse to a first order semantics. We associate logic with the masculine and its punctual nature. We associate semantics with the feminine and its extensive, non-punctual nature. Semantic expresses itself in the form of oppositions between contraries. In the case of first order semantics, there is only a single opposition involved. On the other hand, with second order semantics there are two oppositions, often involving one opposition applied to itself. The traditional left side sciences, including mathematics, only use first order semantics.
Traditional left side mathematics only uses semantics of the first order. Mathematics constructs its semantics from the fundamental opposition between a collection on one side of the opposition, and the objects making up the collection, on the other. This leads to Set Theory, the general expression of first order semantics for practically all of mathematics. The Set is on one side of the opposition and the Elements of the set are on the other. The elements of the set provide some kind of primitive notion of extent. For example, the set of points making up an interval of the real line, is such an example of extent. It is quite remarkable that this is the only semantics that axiomatic mathematics really needs. Feed it Set Theory and off it goes. No fuss.
It is equally remarkable that all of the traditional sciences of our day are based on first order semantics and second order logic. These sciences operate under the heading of the neon light, flashing MF typing of knowledge. It would appear that this kind of knowledge is favoured by those ethnicities that belong to the Christian tradition, cultures with an MF disposition.
We now turn to knowledge of the FM type. According to our analysis, FM type knowledge is based on second order semantics and first order logic. From a linguistic-cultural point of view, we have associated the FM disposition the Islamic tradition supported by the Semitic language Arabic. However, from a philosophical point of view we are lead to the Stoics. The Stoicism was the “least Greek” of the ancient Greek philosophies. Moreover, all the early founders such as Zeno, Cleanthes and Chrysippus, were all of Semitic origin. Thus the cultural typing of Stoicism might justifiably be classed as having “Semitic tendencies.” Be that as it may, we type the knowledge speciality of the Stoics as being of type FM.
The Stoics had their brand of first order logic and they consistently expressed an aversion to employing second order logic and its attendant preoccupation with abstraction. The Stoics only reasoned in particulars arguing that generalisations do not exist. Socrates can exist but Man and mortals do not. There is no such thing as Man. There is no such thing as mortals. Abstract generalisations do not exist. They rejected the species and genus of Aristotle saying that they had no need for them. In modern mathematical terms, they rejected sets. All of modern mathematics is based on sets in the form of Set Theory. Without Set Theory, there can be no traditional mathematics. If a Stoic were alive today, he would still reject Set Theory. The Stoic has no need for such abstractions. The Stoic is content with the logic of Chrysippus, which faithfully avoids anything but the particular. After all, only particulars can exist and that is what concerns the Stoic.
Of course, traditional mathematics goes the other way and reasons over the elements of an abstract set of objects, the set of green apples, the set of prime numbers, for example. First order logic avoids such abstract thinking and only talks about qualities relating to the existence of a particular entity. In their purest form, the qualities involved have nothing to do with the greenness of apples or even the primeness of a number. The qualities are the generic qualities of the generic entities. What matters is whether one has or possesses the quality or not. “if you have the first and the second quality …” is the premise of Chrysippus’ first of the five undemonstratables. The logic does not say what the quality is, but rather whether it is or is not. Relative to you, the quality is if and only if you happen to have it possession at the time. This is an ontological logic. Despite avoiding abstraction, the first order logic reasoning of the Stoics becomes surprisingly profound, as explored in the appendices.
We now turn to semantics. Before moving on to second order semantics, we take another look at semantics of the first order.
Firstly, who uses first order semantics? We know that modern mathematics uses first order semantics and only first order semantics. We notice that this statement did not make the reader suddenly sit bolt upright, which is the reaction we wanted. In fact, the reader’s eyes seemed to have even started to glaze over. In search of a more engaging means of explanation, we come back to earth where people and things actually exist, and not just in the imagination.
We remark that if one looks around us hard enough, one will surely discover an acquaintance, a relative even, who only uses first order semantics in their everyday life. Such people are easy to spot. Moreover, not all of them are mathematicians. The key giveaway is that the person concerned is totally incapable of putting themself in someone else’s shoes. For example, such a person is incapable of putting themself in your shoes. In order to accomplish such a feat, one needs second order semantics. In brief, first order semantics implies a total lack of empathy.
The inability to put yourself in someone else’s shoes leads to the worldview that you are the centre of the universe. This is an inevitable consequence of a first order semantics view of the world. The most famous exponent of this worldview was Ptolemy, of the first century AD. Ptolemy was a gifted mathematician that wrote on many scientific topics. The most famous was his geocentric model of the world based on a set of nested spheres. This incredibly complicated system held sway for over a thousand years until finally replaced by the much simpler heliocentric model.
One wonders whether there are any extremely over complex Ptolemaic scientific abominations around in modern times. One does not need much prodding to come up with a likely candidate. String Theory. Perhaps we should express our admiration for the String Theorists. Their achievements are even more laudable when you realise that they have accomplished so much, and only using first order semantics.
The above explanation of first order semantics is probably as clear as mud. Perhaps we will have to turn back to mathematics itself to bring some sort of rigour to bear on the question. We must turn to the empathy free zone of modern mathematics.
Without going into details, we can say that the kind of mathematical geometry possible with first order semantics is rather trivial compared to the geometry possible with higher order semantics. This is very important as we rely on mathematicians to describe to us the shape of the universe we live in. However, no mathematicians or mathematical physicists to our knowledge have ever pointed out the fine print in their deliberations. They simply inform us that, as a consequence of applying their mathematical theories, it turns out that the world is shaped in this or that particular way. Nowhere in the description is the caveat that, by the way, the expressed views herein have all been based on first order semantics and only on first order semantics. Sadly, there are no labelling laws for modern mathematical products. This must change.
So what kind of geometry do you get when you only use first order semantics? The answer is surprisingly simple. Some mathematicians even boast about how simple it is. They see it as a triumph of applying abstraction. To begin with, they claim that all spaces are n dimensional. Mathematicians cannot stop themselves from generalising. The letter n is a very general number. That way you cover all bases and so it is hard to be wrong. Then comes the decisive factor. All the various mainstream versions of space mathematics have exactly the same geometry! Technically, they all have the same affine geometry. This is truly remarkable. Lines behave like lines and points behave like points in all these vastly different mathematical spaces. The only difference from one mathematical version of spatiality to another is the distance between points. Mathematicians handle this detail by ascribing a different metric artifice, called a metric tensor, to each space. In this way, for example, an ordinary Euclidean space can become Minkowski spacetime geometry by simply swapping the metric tensor.
Practically all these mainstream mathematical spaces are special cases of a Hilbert space, and so the construct goes back to David Hilbert. A ferocious critic of Hilbert was the great Henri Poincaré. Curiously, as an aside, Poincaré was ambidextrous. We could certainly say that about his mathematics too, but he was both genuinely left and right handed with the pen and, it appears, also with the mind. The ambidextrous Poincaré goes head to head against the (presumably) right handed, left paradigm dominant Hilbert: it is a nice image albeit without any grand significance..
Anyhow, history has it that the abstract axiomatic geometry of Hilbert eventually prevailed over the objections of Poincaré. However, the battle is not over. Armed with the realisation that the Hilbert kind of geometry is only based on first order semantics and that there is our second order semantic alternative, the picture may indeed rapidly change. However, this next time round, there will be no conqueror nor conquered. The only thing to settle will be as to which side of the semantic equation is the Master and under what circumstances.
In brief then, mathematics relying on first order semantics results in a very simple, abstract kind of geometry. Simplicity is always an admirable quality when it comes to scientific explanations; according to Ockham’s razor the simpler the better, However, the simple always runs the risk of falling into the abyss of being simplistic. Ptolemy’s thesis that the earth was the centre of the universe was also simple, but looks at the headaches that gave him, and all the poor astronomers that followed him for a thousand years. Modern day String Theory theorists utilise the simplicity of a geometry based on first order semantics and seem to get the same kind of headaches. It is out of our expertise to criticise the details of their work, but looking from afar, it might be that things could be simplified by a paradigm shift or two.
In the appendices of our book, we look at geometry based on second order semantics. In the process we are lead to alternative interpretations of imaginary numbers, the basis for any fundamental geometry. In fact, we are lead to back to our starting point. The imaginary numbers interpreted as MF, FF, and FM typed entities! These same typed entities can be interpreted from a spacetime geometric perspective as cones and heaves of lightlike, timelike and spacelike arrows. In addition, we investigated the enigmatic MM typed entity and intuitively started to understand it as a flip-flopping Figure-Ground, “is” and “is not” kind of geometrical dimension.