Aristotle and the Square of Oppositions

When it comes to logic, the best place to start is with Aristotle. As well as being the greatest philosopher of all time, Aristotle was also the greatest fence sitter of all time. With him, our neat dichotomy between left side and right side thinking meets a blank. This man has a foot firmly placed on both sides. Nowhere is this more apparent than with his categorical logic and in particular his square of oppositions. In this section, without going into too much detail, we summarise the aspects that immediately concern our project.

We end this chapter by presenting an alternative approach of breath taking simplicity and elegance, that pioneered by Chrysippus, considered by many to be Aristotle’s equal. However, to understand the full significance of Chrysippus’ approach, we will need to add some important clarifying innovations on our part that will not be found anywhere else. This is quite an important chapter. If the reader has progressed this far into our exposition, it will be well worth the effort to understand what follows, even for logic specialists. Great beauty lies ahead.

What follows is not rocket science. Each step is easy to understand. The hard part, as always, is to grasp the full significance of the matter.

Aristotle’s Organon

Aristotelian logic occupies a central place in what is nowadays called classical logic. This was the logic studied by the learned peoples, mainly monks, of medieval Europe for a thousand years. During this time, the notation was refined and elaborated, but the essence barely changed. Even by the Enlightenment, Kant was known to exclaim that the only logic that one needed to know was that of Aristotle.

Aristotelian logic was a central component of what he called the Organon, Greek for tool or organ. Syllogisms are logical arguments made up of three parts, a major premise, a minor, and a conclusion. The most famous is the very familiar:

Major: All men are mortal

Minor: Socrates is a man

Conclusion: Socrates is a mortal.

Aristotelian logic is sometimes referred to as term logic where each proposition of a syllogism is made up of two terms. What interests us is how many kinds of term are necessary for such a logic. This also interested Aristotle. He argued that there were four distinct kinds of term. During the Middle Ages the Scholastics gave each a letter as shown below.


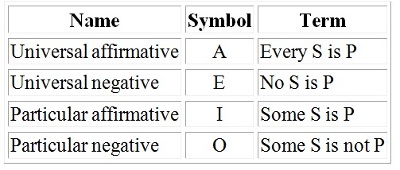
Figure 26 The four kind of terms. The Scholastics later labelled them with four letters.

The Four Terms and the Left Side

Aristotelian logic was half modern and half ancient. We will suspend judgment on which was the better half. The modern half is exhibited in two ways: it relies on abstraction and its logic is static. The abstraction can be seen in the use of the existential qualifier “All”. “All men” for example, means every man. By referring to “all men” or every man, one is referring to an abstraction, a generalisation. As the Stoics pointed out, abstractions and generalisations do not exist. In addition to abstraction, there is the fact that the logical representation of these syllogisms can be covered by Venn diagrams as shown below. The terms can be said to have “Venn Diagram” semantics. This characterises the logic as a static, synchronic mechanism.

Both of these aspects, the abstract and synchronic nature of the logic, are characteristics of left side thinking. By default, left side thinking has become synonymous with the modern.

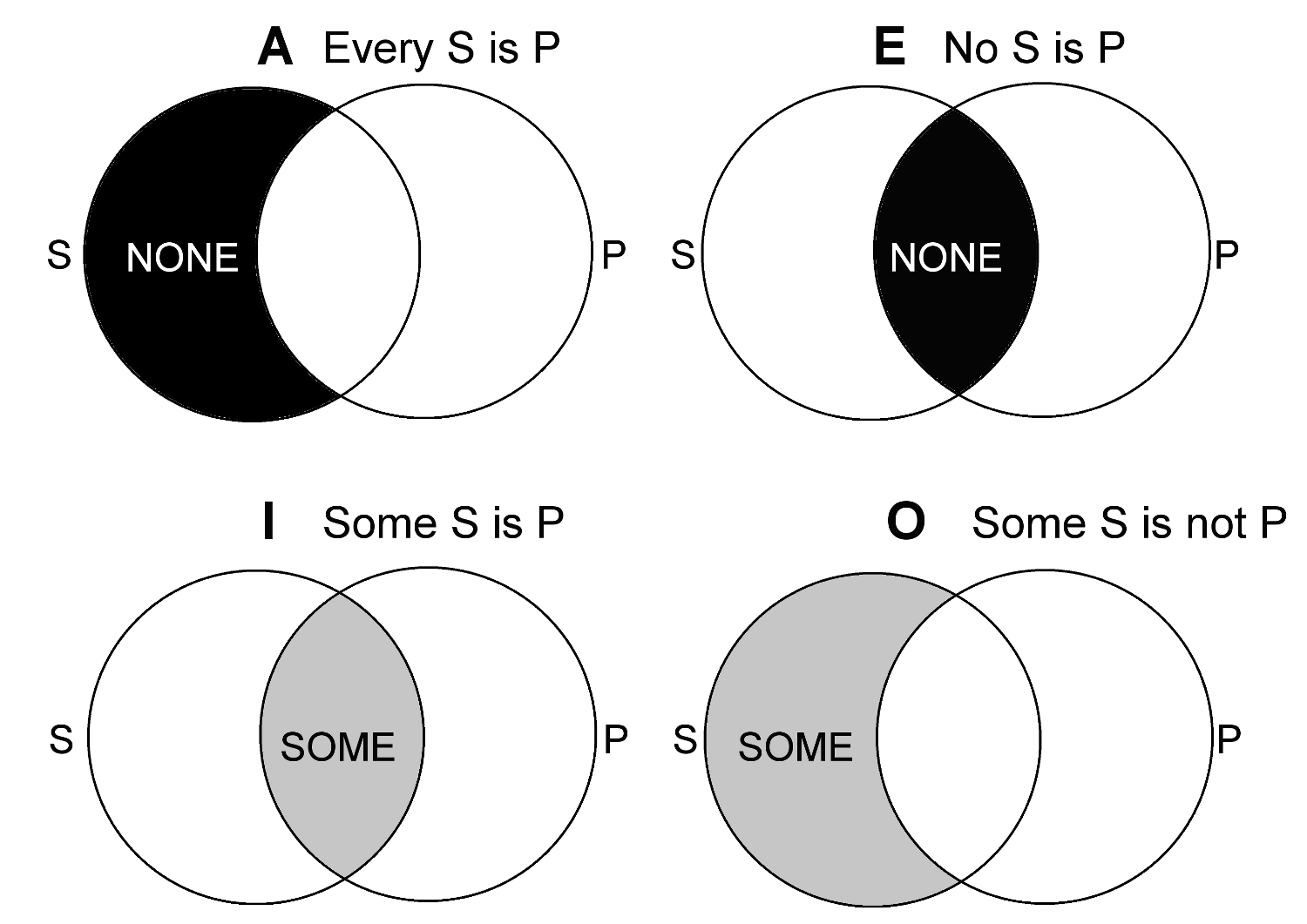
Figure 27 Venn diagrams for the four terms of Aristotle

The Four Terms and the Right Side

However, what is not modern in Aristotle’s logic is that his infrastructure of the four kinds of terms is not determined by a set of axioms, but rather by a pair of oppositions and the opposition between these oppositions. This is exactly the approach we have been using to construct our semiotic squares. Firstly, obtain a pair of oppositions. Employ one opposition to define a left right dichotomy and the other opposition for the front back structure.

In Aristotle’s case, the left right dichotomy is a strict logical opposition between the affirmative form and the negative. The second opposition is between the universal and the particular. Both these oppositions must be true dichotomies in order to construct a non-trivial semiotic square. This is a technical point, but a very important one and will be discussed later when considering Aristotle’s square of oppositions. It turns out that there can be certain cases where an opposition is not a true dichotomy. This can occur when the subject of a term has no existential import. In other words, when dealing with empty sets such as “All centaurs”.

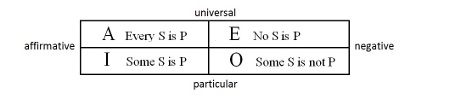
Figure 28 The semiotic square for the four terms of Aristotle’s Syllogistic logic. The square is formed from two oppositions, the negative/affirmative, and the universal/particular.

Superimposing the two oppositions in the one structure, we get the semiotic square as shown in Figure 28 The semiotic square for the four terms of Aristotelian logic. The square is formed from two oppositions, the negative/affirmative, and the universal/particular.

Term Logic

During the middle ages, the scholastics labelled the four kinds of terms with the four letters A, I, O, and E. Syllogisms consist of three propositions, a major, a minor, and a conclusion. Each syllogism could thus be labelled by a triplet of letters taken from the four-letter AIOE alphabet. This fascinated the Scholastics and, many years ago, entertained the author’s curiosity for some time. The reason for the author’s interest was that such a system did have some resemblance to the triadic structure of codons in the genetic code. With a bit of effort, one can make some kind of rapprochement between the AIOE alphabet of the scholastics and the genetic-cum-generic AUGC alphabet, but the effort is probably not justified, as there are richer pickings elsewhere, notably in Stoic logic.

The genetic codon structure only has 64 combinations. What we have ignored for the syllogism is the detail of how the three propositions in each syllogism hook together. We have ignored the fact that there are four different figures of the syllogism. Thus taking into account the four figures, instead of 64 possible syllogisms there will be 256. Only nineteen of these syllogisms are regarded as leading to a valid conclusion.

Aristotelian logic provides a logical tool that is applicable to the contingent world. Unlike modern logic, it also brings with it some nontrivial semiotic infrastructure, the square of oppositions.

(see my online syllogism machine for exploring Aristotelian )logic.

The Square of Oppositions

Aristotle described how the four kinds of terms could be placed in a square illustrating the various oppositions between them. He then went about characterising each kind of opposition, although the subalterns were not mentioned explicitly.

The oppositions between universal statements are contraries. Contraries have the property that both cannot be true together. One may be true and the other false. It is also possible that both can be false together. On the other hand, subcontraries involve oppositions between particulars. In this case, both cannot be false together.

Figure 29 (a) The modern logic version of the oppositions. (b) Aristotle’s square of oppositions.

The Modern Square of Oppositions

Of great interest to us is an opposition at a higher level altogether, the opposition between Aristotle’s syllogistic structures and modern logic. The dramatic difference between the two approaches was clearly illustrated by George Boole, in what has become the modern version of the Square of Oppositions.

Modern logic differs from the ancient logic by simply replacing the universal with the general, in other words with the abstract. This can be achieved by using labels and the logic becomes symbolic logic. Thus, the term ‘All men’ is replaced by the abstract version ‘All X’. The thing gets replaced by a label and introduces different semantics. The label becomes simply a placeholder and as such, like any placeholder, may be empty. The logicians explain this as relaxing the requirement of existential import. From a classical mathematics perspective, the generalisation introduced by modern logic is to allow sets to be empty.

Once the reasoning becomes abstract, the logical difference between yellow centaurs and canaries evaporates. Not only that, but all the oppositions except the contradictories have also evaporated. For example, both sides of the contraries opposition ‘All centaurs are yellow’ and ‘No centaur is yellow’ are true. The contraries opposition has evaporated.

Figure 29 (a) shows the resulting modern logic version of the square of oppositions. The square has virtually collapsed and only the contradictories and the subcontraries survive. We have deliberately drawn the modern version on the left side relative to Aristotle’s square to illustrate that this is the left side variant of logic. The other variant is Aristotle’s seed for the right side version. The left side involves abstract, symbolic logic. The right side in the diagram represents Aristotle’s version of elementary generic logical structure. In practice, the modern symbolic logic approach boils down to a simple bipolar nominalism where the basic opposition is between two particulars, I and O. The letters A and E act as pure label signifiers for the I and O respectively, acting as the signified. The contradictory oppositions A-O and E-I model the relationships between signifier and signified. In essence, the system becomes a simple two letter system labelled by A and E. Thus, although we have not shown that modern day logicians only use half a brain, we are starting to see that they reason using only half an alphabet.

This is our first exploit into the differences between abstract, symbolic logic and generic logic. We can do better. This will be our task in the next section where we investigate Stoic logic and discover great beauty in the land of Chrysippus.

Generic Logic and the Stoics

In this section, we are going to look at the Stoic version of Square of Oppositions. This will undoubtedly upset the scholars. There is no explicit record that the Stoics ever proposed an alternative to Aristotle’s Square of Oppositions. However, we are not constrained by historic Stoicism. If something is missing from the puzzle then we must endeavour to reverse engineer it. We attempt to follow in the tradition of Chrysippus himself, of whom it was said:

… in many points he dissented from Zeno, and also from Cleanthes, to whom he often used to say that he only wanted to be instructed in the dogmas of the school, and that he would discover the demonstrations for himself. (Laërtius)

Stoicism, particularly the Early Stoa, is a very tightly integrated body of thought, much tighter than what might be imagined, especially after Chrysippus had a hand in the matter. Traditionally Stoic philosophy involves a tight integration of physics, ethics and logic. Likened to an egg, the yolk was physics, the white ethics, and the shell was logic. Logic protects and holds it all together.

Stoic logic differs dramatically from that of Aristotle. There is no static classificatory apparatus. There are no species and no genera. There is no extension or comprehension of terms. The figures and modes of the syllogistic evaporate into thin air. To the Stoics, Aristotle’s syllogistic logic was “useless.” (Chénique, 1974) In contrast, Stoic logic is starkly oriented to the individual. As such, it incorporates one aspect that might entitle the logic to be considered a generic logic, a logic free from abstraction. It is this kind of logic one needs to construct and deconstruct a real world, not an abstract world. However, what precisely is a generic logic? Our immediate task is to answer this question. Now proficiency in logic demands a certain dexterity and agility of the mind. In this respect, the author has been blessed with a mind as nimble as the Titanic and just as infallible. This helps explain his reaction when thirty years ago he first came across Stoic logic. Almost nothing is left of Stoic texts in modern times. Nevertheless, a rough sketch that can be coagulated into less than a page or so has survived. It was Chrysippus’ Ground Zero, viewed from a logician’s point of view of course, a great logician’s point of view. The author was quite excited: it is not every day that one comes across an explanation of the structure of the Cosmos spelt out in hard-core logic, all on one piece of paper to boot. There they were, Chrysippus’ five logical undemonstratables. According to Chrysippus, all reasonment stems from these five logical gems. The author stared at the five gems like a stunned plover. If this is it, he could not see it.

Over the years, the author came back numerous times to the five undemonstratables in an attempt to really ‘get it’. A favourite reference was Éléments de Logique Classique (Chénique, 1974). The pages were getting quite dog-eared. Each time brought about the same stunned plover reaction. He still did not get it. However, Chrysippus’ third undemonstrable stuck out a bit from the other four. It looked very much like the modern logic operation called the Sheffer stroke, named after Henry M. Sheffer. It is called a stroke because that is the way it is symbolically written, as a vertical stroke. The author would look stony eyed at the third undemonstrable and ask himself: “What does it mean?” He knew that if he asked someone trained in logic they would patiently, and perhaps condescendingly, explain that it means “NOT this AND that”. In plain English, it means not both. It is sometimes called the NAND operation. It is important in logical networks because any network can be built uniquely using NAND gates. In other words, any other logical operation can be built up uniquely using NAND. They would then go on to explain that Charles Sanders Peirce had earlier in an unpublished work (Peirce,

1880) come up with the mathematical dual which is now called the Peirce Arrow, written as a vertical arrow. This is the logical NOR operation. Such thoughts would make the author’s eyes glaze over. He would ask himself, “But,what does it really mean? What did it mean to Chrysippus?” Superficially, it simply looked as if Chrysippus was the first to discover the propositional calculus. Granted he had made the discovery several thousand years in advance of the moderns, but this is the kind of thing one would expect from a master logician. If that was all there was to it, then Chrysippus would have nothing much more to offer the moderns. The undemonstratables could be simply seen as an early attempt to systemise and even axiomatise the propositional calculus. Chrysippus could be brought into the modern camp and branded as one of them. Surely, there must be a deeper message here.

For a long time, Stoic logic remained as a kind of lurking nemesis in the author’s mind. The five undemonstratables, where did they come from? What is the underlying principle? For a philosophical system as tight and unified as the Stoic’s, the logic must have the same basic epistemological and ontological signature as their physics and ethics.

Our approach so far has been based on an intuitive interpretation of how the physics and ethics could be constructed from a fundamental ontological dichotomy. The dichotomy can be understood linguistically as the difference between the verbs to have and to be. Two fundamental entities were proposed that expressed primary difference free of any accidental, empirical attributes. In this scenario, one entity had the attribute of being devoid of any specificity whatsoever whilst the entity was this attribute. One entity has an attribute; the other entity is this attribute. The difference between these two entities was said to be a difference in gender. Using this gender construct, the primary attributers of reality can be constructed from first principles. The attributes are not harvested empirically, but synthesised, calculated.

We note in passing that our gender terminology is more reminiscent of Indian and Chinese philosophy traditions. Rather than explaining the beginning of a creation cycle in terms of a union between the feminine and masculine, the Stoics tended to restrict their vocabulary to the masculine register, where only Zeus and his seed seem to feature. For the Stoics, the two principles translate to the active and the passive principles. We prefer reading this as the masculine and feminine principles because, in this relativistic domain, the gender concept is much more generically neutral. What is active can be passive and what is passive can in turn be active.It is much easier to talk in terms of gender where the masculine can play the role of feminine to produce the MF type for example, and vice versa. At any rate, all of this is just a debate about terminology. Using Ockham’s razor to cut through the debris, we will stick to the simple and clean gender terminology as the basis for our generic science. Maybe some Stoics did too.

The approach leads to the four elementary letters of the ontological alphabet based on the binary gender typing MF, FF, FM and MM. For reasons that will later become apparent, we allocated the letters A, U, G, and C respectively from the genetic code for this four-letter ontological alphabet. The detailed algebra of this ontological code based on this fourletter alphabet has yet to be determined. This code is capable of describing and proscribing any being whatsoever, including the universe, itself a being. Any being must have its own ontological DNA, so to speak. It is in this way that a being can be sure of what it is.

Using this gender construct, the theory of the four ontological elements can be explained in terms of four kinds of substance typed by the binary gender typing MF, FF, FM and MM. This corresponds to the ancient terminology of air, earth, water and fire respectively. If it starts with M it’s light stuff, if it starts with F it’s heavy stuff and so on, according to the ancients.

The four elements have multiple instances, are mobile, and mix. The four binary types also apply to something that is not mobile and is located at the centre of the universe; or rather, at the centre of its universe. This is the generic subject, what can be thought of as any being whatsoever. This is the generic template of mind. The whole universe gyrates around this entity. Not only are the four typed bodies fixed at this location, they are fixed in relation to each other. The two bodies with a binary gender starting with M are located on the right and the F on the left. The two bodies with gender typing ending in M are located in the front lobes, the F in the back. The question regarding telling the difference between left, right, front and back can be resolved by looking at the gender typing. This might seem a bit tautological, but that is the way things work in this world. Here relativity is not only endemic it is generic.

At this point in the game, there is also the question of whether the four kinds of mobile elements circulate to the exterior of this generic mind or in the interior. This question cannot be answered at this stage of the ontological development, as what is interior to subject and what is exterior is still unqualified.

Finally, we come back to the main question in hand, the Stoic logic question. What is the ontological interpretation of Chrysippus’ five undemonstratables?

The Fifth Element

In order to answer this question, we have to start thinking in terms of quintuplets rather than just quadruples. Before we tackle the logic quintuplet, it is worthwhile looking at Stoic physics. What is the fifth element?

Aristotle argued for a fifth element in his physics, which he called aether. A fifth element was necessary to fill the heavens above the terrestrial world and to explain the constant, unchanging rotation of the stars.

The Stoics also added a fifth element to their system, calling it pneuma, an ancient Greek word meaning ‘breath’. In this perspective, the four elements air, earth, water and fire were considered passive, whilst the pneuma expressed the active principle. Unlike Aristotle’s aether, the pneuma permeates everything and expresses the Logos for both the Cosmos and the body.

Some accounts say that pneuma is created from the fire and air elements. From our previous analysis, we know that the fire and air elements of antiquity have the gender coding MM and MF respectively, which indicates a primary gender of masculine for both. For the Stoics, the masculine gender was interpreted as embodying the active principle, which would explain fire and air being associated with the active principle. The other two elements water and earth are gendered as FM and FF respectively and so are primarily feminine and hence considered as embodying the passive principle.

So far, we have provided the fundamental ontological justification for the ancient four element based physics that was adopted by the Stoics. However, there was no trace of any fifth element in our development. A clue to the missing fifth element can be found in Chrysippus’ five undemonstratables, in particular, the third undemonstratable. As for the other four, we will use them to resurrect a square of oppositions for the Stoic logic of Chrysippus that is comparable to that of Aristotle. Just as the medieval scholars gave four letters to the four terms of the Aristotelian square, we will do the same for the logic of Chrysippus. However, instead of the medieval AIOE lettering we will use the AUGC lettering of the generic-cumgenetic code that we are developing. As for the fifth term, it has no letter. There is no fifth letter in the genetic code. There is no fifth letter in the generic code.

In the biological genetic code, the AUGC lettering based on the codon triplets of letters, code amino acids that go to making up protein. There is no sign of any fifth player in the scheme of things. Moreover, there is no need to try to find a fifth player as it has been there right from the beginning of our development. It forms the core of the very essence of gender, the generic building construct of anything that aspires to be.

To be what one is does not come easily. Being is not something handed out on a plate. To be requires Oneness of the being in question and it is up to that being, and that being alone, to maintain and express its own Oneness.

Generically, this is expressed by the generic entity characterised as totally devoid of any specificity whatsoever. This total lack of specificity must be the case as the generic entity can be anything whatsoever. Such an entity acquires Oneness by interaction with a subject. The subject may imagine it, think about it, touch it, measure it, claim it, or whatever the interaction, the result is that of a collapse to Oneness relative to the subject. Relative to the generic entity itself, the Oneness arises from the one single characterising attribute that the generic entity possesses, that of the absence of any qualifying specificity. The irony of the situation is that this total lack of qualifying specificity plays the role of attribute. The generic entity has an attribute. This attribute that the generic entity has, if it is not to violate First Classness, must be an entity in its own right. This entity is the attribute. Thus, there are two different entities, which share the one single attribute. One entity has this attribute; the other entity is this attribute. The difference between these two entities can be thought of as a difference in ontological gender. The entity that has the attribute is feminine, whilst the entity which is the attribute is masculine.

The masculine entity endows Oneness. As attribute it is pure singularity, pure Oneness. The remarkable thing with the resulting science that can be built upon this initial union of the feminine with the masculine is that entities that are more qualified can be constructed, based on compound gender typing. The first compound types are the four binary combinations of the feminine and masculine and can be considered as the four fundamental “letters” of the generic code. Thus, the four compound genders MF, FF, FM, and MM are allocated the letters A, U, G. and C respectively. The arguments for this particularly allocation will be advanced later.

Ontological gender appears, albeit informally, in the cosmologies of the many different civilisations from the West to the East and Far East and beyond. In this work, we present a formalised version of the construct. The formalisation is not an abstract axiomatic, but a formalisation of a different kind, the generic formalisation. The generic formalisation leads to a new kind of science that we could call generic science.

The essential ingredient in such a science is the rapport between the feminine and the masculine. These two gendered entities are different, but indistinguishable. They are indistinguishable because there is no way to compare them: they both share the one single attribute between them. The attribute that they share is that of Oneness: one has it, the other is it. There is a tension between these two entities. If ever the bond between them were broken, then that would spell the end of the world, at least for it.

The tension between the two genders expresses itself at the microscopic level between all the individual masculine-feminine compounded gender typing of a complex organism. Threats to Oneness of the Organism abound at all levels. This complex compounding of tensions throughout the organism is probably what the Stoics referred to as the pneuma.

We will continue our discussion of the pneuma, this mysterious “fifth element” further on. In the meantime we take another interlude to hammer home the intuitive understanding of the simplest but most profound concept of all, that of ontological gender.

A Light Interlude

Gender is not an abstraction. Any being is it and has it. Any individual being is gender typed. Once again, this is not an abstraction. For example, every cell in an animal’s body contains a copy of its chromosomes consisting of long strings spelling out the genetic coding of the individual. The coding is built up of words consisting of triplets of the four letters AUGC (using the RNA convention). From a gender perspective, the genetic coding has a deeper structure than that determined by biochemistry. The four letters can be represented in terms of binary gender typing MF, FF, FM, and MM respectively. Thus if the reader wants to know his or her gender typing then all they need to do is to translate their AUGC based genome into the gender equivalent.

Gender can be illustrated more concretely than even this biological version. Consider the following two rather tongue in cheek examples of gendering. The examples may help to overcome the bad habit of always thinking with a left brained mental disposition. Each example aims to prove once and for all which gender is superior to the other. The reasoning is only vaguely inspired by the Hindu Naya five-step syllogism and so lacks some of the rigor.

Proposition 1

The masculine gender is superior to the feminine gender.

Example:

Take the case of a bird in the hand and the birds in the bush.

Analysis:

The bird in the hand is of masculine gender as it is in possession of the subject, a fact that is absolutely and even tautologically true because the bird is in the subject’s hand. Conversely, the birds in the bush are of the wildcard species, not in possession, and undoubtedly hard to catch. These birds are obviously of feminine gender.

Proof:

In order to prove the proposition we invoke the age-old proverb:

A bird in the hand is worth two in the bush.

Conclusion:

This goes to show that the masculine gender is superior to the feminine (by at least two times).

Not to be out done, there is another argument, which demonstrates the converse.

Proposition 2

The feminine gender is superior to the masculine gender.

Example:

Take the grass on your side of the fence and the grass on the other side of the fence.

Analysis:

The grass on your side of the fence is of masculine gender as it is in possession of the subject (which is you). This fact is true for tautological reasons. However, the grass on the other side is not in the subject’s possession, and remains tantalising out of reach, a real wildcard. That grass is obviously of feminine gender.

Proof:

In order to prove the proposition we invoke the age-old proverb:

The grass is always greener on the other side of the fence.

Conclusion:

This goes to show that the feminine gender is superior to the masculine gender (and much more desirable).

There is another variant of proposition 2 that employs the notion that the spouse on the other side of the fence is more desirable than the spouse on this side of the fence. We will not go into a detailed analysis of this case, but the variant has some value as it goes to show that gender is only obliquely related to sex. A spouse of one sex can be gender typed masculine or feminine, depending on context.

The Gender Algebra of Oneness

As we have said often, left side sciences are based on abstraction, dualism, empirical attribute harvesting, and employ a labelling, categorising, taxonomic epistemological technology. Right side science replaces the abstract with the generic, dualism becomes a monism and the attribute harvesting from the field and laboratory is replaced by attribute construction from one single attribute based on the generic gender construct. As for epistemological technology, labelling, the linear descriptions and essentially rhetorical approach of left side science give way to the dialectical where concepts and semantics are expressed in purely relative terms. Concepts and constructs are expressed in the form of oppositions. Moreover, whilst left side science specialises in the tunnel view of reality, right side science must always address the whole.

Right side science must always take the holistic view. This is the essence of monism; nothing can be left out of the picture. This means that right side science always deals in wholes. A whole is totality viewed from a particular point of view, the point of view of the present subject. The subject is always present in right side science. In the traditional left side sciences, including mathematics, the subject is always absent. As such, left side science specialises and only recognises one-half of reality: it is half-world science.

Right side science must be a monism. There can only be one such science. The Stoics were pioneers in this area with their unified version of the monism, and we follow in their tradition. However, we make no attempt at doctrinal orthodoxy.

The incredible thing about right side science is that it is independent of scale. One still sees the universe as a whole from even the most apparently microscopic point of view. The science is in fact starting point invariant. It does not matter where you start; you always get the same science. There is one and only one science with this unique property. As a theory, the theory is its own invariant.

The science is independent of scale and independent of starting point. It does not matter where you start; you always get the same theory: That is the theory.

Generic Coding

Left side sciences are dominated, even swamped by an ever-increasing avalanche of attributes. Contrast that with the attributes in Generic Science, the right side science. There is only one attribute for the whole science! This single attribute is the attribute that the pure feminine F has. It is the pure masculine M. The feminine has an attribute. The masculine is that attribute. That defines what gender is all about. One entity has it; the other is it. All other attributes are simply built up from different combinations of the masculine and the feminine.

It might be thought that the feminine F is also playing the role of attribute, which of course it is, but only by role-playing it, not being it. And so here is the difference. We can be absolutely sure of what the masculine attribute means. We understand the masculine as it means one and only one thing. It means pure Oneness. It represents pure certainty, because we know what Oneness means. The situation with regard to the feminine is the opposite. It represents the opposite of certitude. It represents total ignorance. We do not have a clue of what the feminine actually is, not a clue. This is the absolute expression of the Uncertainty Principle. It is also the secret of Generic Science. Generic Science is the only science that can talk about something that it knows absolutely nothing about, and talk about in absolutely certain terms. Moreover, it can express its ideas in algebraic form.

Now the reader may have had a similar experience to the author as in the following. The author remembers vividly, many years ago, when his Technical School mathematics teacher started the day’s lesson with great drama, something he was prone to do quite often. His name was Harry Sermon. Harry wrote up on the blackboard one letter. It was the letter x. Now apparently x was just like a number. Apparently, you could add it, subtract it, multiply by it and so on; remarkable. Even more remarkable was that you could do all this without having a clue of what the actual value of the number x was! Remember that? The lesson of course was an introduction to elementary algebra. Now having gone through what we now realise was not a complete waste of time, we find ourselves faced with the prospect of learning the algebra of the Cosmos, a worthwhile enterprise surely. Instead of the letter x, we have the ultimate unknown of all time and possibly even outside time, the letter F. This is the wildcard of the cosmic algebra. Its value can be any entity whatsoever. In the case of x in our first algebra lesson, at least we knew it corresponded to a number, even if we did not know its value. In the case of F, we do not have a clue about anything, whether it is a number or god knows what.

Our project is to develop a way of describing our pure ignorance of the world. Now some people might say that if you do not know what you are talking about then you should shut up. However, we take the high road, the road of Socrates’ confession of ignorance. He is reputed to have said that the only thing he knows with absolute certainty is that he knows nothing with absolute certainty. In addition, this is our position; and our task is to develop algebra up to the task of expressing such wisdom.

One of the main points made in this work, is that we have apparently been beaten to the gun. Instances of the algebra, the algebra of Socrates’ confession of ignorance, are everywhere. In your body, repeated in every cell is the same description over and over again, of what you are and are to become. All that has to be done is to “solve for F”, based on the situation on hand. The question, ‘Why bother?” may be raised by those not motivated to solve things, particularly algebraic things. It is a good idea to solve these Socratic gems of wisdom, as a failure to do so may challenge your very existence. If your body gets its Oneness equations tangled up, you could be in real strife.

…

Only two letters are needed for this code, the letter M and the wildcard F. Combined in pairs they make up the four letters of the alphabet of the generic, pardon, the genetic code. These are the letters A, G, U and C, all binary compounds of F and M. The macroscopic organism is organised as an immense compound articulated by these four letters, an immense compound of F and M gendered entities. M expresses the Oneness of the organism, F the unqualified, the unknown, “Solve for F”, and perhaps you have your life in a nutshell. However, solving for F may take a lifetime and could depend a bit on what crops up along the way.

Before understanding our reconstruction of the Chrysippus semiotic square, we need to know a bit about semiotics , or at least, our version of it.

The author’s first acquaintance with the semiotic square came from following the courses of Greimas back in Paris, many years ago. The term “semiotic square” is nowadays generally associated with his name. The big weakness in the Greimas approach was his failure to come to terms with the subject. His semiotics
is sans sujet. We will sketch out here a more fundamental approach to semiotics
and the semiotic square that does include the subject.

To begin with, there are two kinds of semiotics
, one associated with Ferdinand de Saussure (dyadic, arbitrariness of the sign etc.) and one associated with Charles Sanders Peirce (triadic). In our view, the approach of de Saussure is not semiotics
, but General Linguistics. Like Greimas, the approach of de Saussure is sans sujet. If there is a subject, it is part of the Spectacle, not the Spectator. It is merely what Hegel referred to as the empirical ego. In this perspective, the de Saussure approach is like that of the traditional sciences and mathematics. All of these sciences are sans sujet. We call all of these traditional science left side sciences. Left side sciences claim to be objective, which is another way of saying that they only concerned with a reality of objects where any reference to the subject has been excluded. They are all sans sujet. As such these sciences look at the world from a very specific point of view. This point of view has been described as the “view from nowhere” or the “God’s eye view”. This is a general characteristic of science sans sujet. It is a general characteristic of all the sciences and mathematics of today.

The other possible scientific paradigm goes in the opposite direction. It demands that the subject is always present. In other words, if there is a spectacle there must also be an accompanying spectator. You can’t have one without the other. We call the science based on this paradigm, right side science. The right side science becomes, in fact, the dialectic of the Spectator and the Spectacle, the Subject and its kingdom.

Unlike the many left side sciences, there is only one right side science. This is because its focus is on the science of the subject and this is quite different to the science of objects. It is the science of the Self. For a Stoic logician like Chrysippus, it is the science of the Logos. This generic entity, the Self, the Logos, the Ego, has a generic form. This form can be worked out from pure reason.

Now Charles Sanders Peirce was more inclined to the right side paradigm, but he didn’t make much headway. He also despised the Stoics, which didn’t help. Thus we have to start from scratch. Starting from scratch means that we start with a subject and its kingdom. Alternatively we start with a kingdom and its subject, the same thing. Both spectator and spectacle must be present in the same moment.

This is where we have to put our thinking caps on. The relationship between the Subject and its Other is a very particular kind of relationship. They each determine one another. The Hindus sometimes see this as a coital relationship. The subject corresponds to the masculine and the mysterious other is feminine where gender gets interpreted as sex, poetic licence oblige. The Stoics saw the relationship as that between the Active Principle and the Passive Principle. Vedanta philosophy often refers to the Active principle as the Principle of Individualization, the Spiritual Principle, or simply the masculine principle. We have here the building block for right side science. It’s getting a bit steamy so here is one way to arrive at a dispassionate view. It involves the gender construct.

The main role of the subject in this right side science, is that it does provide a determined point of view. As such it is a pure singularity. What is non-subject is non-singularity. This can be formalised with the concept of gender. The gender concept is very ancient, both in the West and the East. First there is the unqualified substance totally devoid of any determined specificity. Such an entity is typed as the pure feminine. One might say that the pure feminine is devoid of specificity and so has no attribute. This is not the case. It is only devoid of a determined specificity. It has an undetermined specificity. That is its attribute. This attribute, using the argument of First Classness, must be an entity in its own right. (Note that the Stoics always claimed that the property of an entity is an entity in its own right). This attribute entity will be said to be of masculine gender. Two entities, one has an attribute, the other is the attribute. The first entity corresponds to the feminine, the second to the masculine. These two entities provide the building blocks for the right side science paradigm.

The first thing to construct is the semiotic square. One way of understanding this square is as the architecture of a whole. Totality can only be understood from a determining point of view of the subject. Instead of comprehending the totality in any moment, which is impossible, it is understood as a whole. A whole is totality looked at from a particular point view. There are as many wholes as there are points of view. This requires that the subject must be present in the whole. Right side science always understands things in terms of wholes.

Thus the semiotic square, as a generic understanding of a whole, is a map of the subjects conscious understanding of the whole, any whole. The first moment of understanding is “Wow, here I am, this is me and the rest is not me.” We thus draw a square, cut it down the middle and adopt the convention that the right side corresponds to subject and the left side to what is not subject. The right side is masculine typed and the left side is feminine typed.

However, the subject in this particular configuration is not you or I. It represents the impersonal subject. In fact, it is this subject that corresponds to the “view from nowhere”, the “God’s eyes view” of the traditional sciences. These sciences, in their quest for objectivity, remove all reference to subject from consideration. They even remove this impersonal subject from consideration as they have no need for it. They demand a godless science, a pure science sans sujet. Thus the semiotic square for the left side sciences is the same as for the right side science, except that the right side is blacked out. Left side sciences thus suffer from a symptom well known to the psychiatrist. It is called hemi-neglect. Right side science knows about the left side, left side science wings it alone, content with half a brain, so to speak. Curiously, in passing, the human brain exhibits exactly this same bi-lateral specialisation. The right hemisphere does not exhibit hemi-neglect and sees a whole world. Only the left side exhibits hemi-neglect.

This is now where left side and right side science part company. Not content with just the presence of the impersonal subject, right side science must find a way of introducing a more determined subject, the personal subject. This is constructed by applying the first feminine masculine opposition to itself, an opposition of two oppositions. It might sound complicated but is easily visualised with the semiotic square. The second opposition is orthogonal to the first and so instead of a left right dichotomy, the dichotomy is front back. We use the convention of masculine in front, feminine at the back. It appears that we am not the only ones to adopt this polarity convention..
semiotic

The end result is that we end up with a square shaped kind of placeholder for dealing with knowledge. The first kind of knowledge involves an elementary consciousness of self, a knowledge of what is and what is not. This is expressed logically in our reconstruction of the Chrysippus square. For the moment, note that the four parts of the semiotic square have been binary typed with gender. For example, the left front part is typed as MF. This reads that, from the impersonal subject perspective, it is typed as feminine. From the personal subject perspective it is typed as masculine. Thus the first letter in the binary gender typing is that of the personal subject, the second letter is that of the impersonal.

Figure 1 The generic semiotic square is constructed from the feminine masculine opposition applied to itself.

The semiotic square is a placeholder, the architecture of the generic mind, so to speak. The semiotic square is static and unique, for the purposes of the science. You only need one brain, it can be said.

In addition to the placeholder, there are values relative to it. These values are mobile. There are the four kinds of elementary substance that can be binary typed by the four binary gender types. The binary typed substance correspond to MF, FF, FM and MM. The ancients called them air, earth, water and fire respectively.

Stoic Qualia	Pure Gender Algebra	Element
masculine active	MM	Fire
masculine passive	MF	Air
feminine active	FM	Water
feminine passive	FF	Earth

Figure 2 The ancient four elements can be can be understood in terms of gender.

We now come to the semiotic square constructed with four of the Chrysippus undemonstratables. Note that one diagonal is constructed from the conjunctive syllogisms. These are known to logicians as Modus Ponens and Modus Tollens. The other diagonal is constructed from the two forms of the disjunctive. The diagram can be gender typed by matching the is copula with the masculine and the is not with the feminine, as shown. This matches perfectly with the semiotic square gendering shown above.

What is interesting, is that the logic of Chrysippus has introduced yet another dimension into the semiotics
, a vertical axis. The square becomes the “Chrysippus cube”! We have used the convention of the implication arrows in the diagram going left to right to signal the upwards direction, and the downwards for the right to left. Talking intuitively, this indicates that the top two entities have an “upward flow” and the bottom two entries have a “downward flow”.

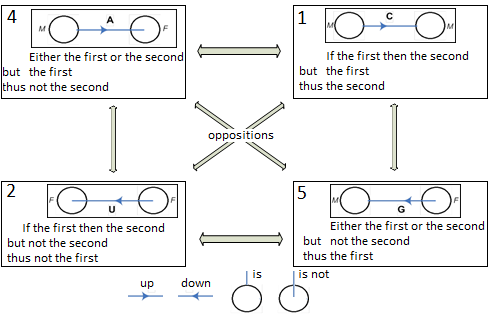Chrysyppus Logical Semiotic Square

One should note that the gender coding of the top two elements correspond to the “elements” of air and fire. These are the “light” elements, being predominantly masculine and less substantial than the feminine bottom two elements of earth and water. Such reasoning is not very rigorous as we are not talking about the same kind of elements as in the left side, traditional science. The logic of Chrysippus however adds a different complexion to the matter.

These principles must have been part of core Stoic teaching, as Marcus Aurelius wrote in Meditations.

Your aerial part and all the fiery parts which are mingled in you, though by nature they have an upward tendency, still in obedience to the disposition of the universe they are overpowered here in the compound mass. And also the whole of the earthy part in you and the watery, though their tendency is downward,

The Stoics claimed that theirs was a unifying science that integrated logic, physics, and morality. Some people are attracted to Stoic values whilst thinking that their science has been completely eclipsed by the modern day sciences. However, how antiquated is the science of antiquity? Consider the following.

In our diagram we have added in the four letters CAUG matching up with the gender typings MM, MF, FF and FM respectively. This is part of another story in this book. These are the four letters of what we call the generic code. We’ve taken them from the RNA version of the genetic code. The genetic code is a standard code which codes all living beings, without exception. This is a known fact. The generic code is impervious to evolution and has remained unchanged since the year dot. By extending the notion of the living to that of the universe, itself considered as living by the Stoics, this same code takes on a generic vocation. In this book we explore its application to understanding elementary particle physics from a new angle (see Appendix). We use the generic code to code quarks and leptons. These claims may test our short term credibility. However, in the longer term that is the way it will pan out once we have properly digested this new science, a science with such ancient roots.