The technical core of the paper will not be presented in the blog.
Formalising Choice
The process of formalising knowledge in the left side science is a relatively straightforward affair. The basic technology is already in place: It is called mathematics. Mathematics provides the tool for formalising the traditional left side science knowledge. When it comes to formalising right side science, one immediately comes up against a brick wall. None of the mathematics works. The obstacle is the draconian constraint of FC. FC must not be violated. The problem is that traditional axiomatic mathematics violates FC right down to its very core.
However, all is not lost. Because axiomatic mathematics is a formal system, it can be exploited to formalise the obstacle to formalising an FC compliant system. Mathematic formalises the way the problem must not be tackled. Axiomatic mathematics formalises the wrong way to go, that is to say, the wrong way to tackle the Kantian problem. Having a formal statement of the obstacle to progress, all we have to do is to find the way around the obstacle. If we cannot do it with mathematics as it stands, we will need something else.
Looking down at the very foundation of mathematics, we come to Set Theory, the elementary mathematic of collections. Without a formal notion of collections of things, there can be no formal mathematics. There are many axiomatic systems that claim to formalise Set Theory. Each system has a different set of axioms, but all systems contain one pivotal axiom, the Axiom of Choice. Faced with a Set of elements, which may even be infinitely denumerable, how can you distinguish one element from the other? How do you choose? The Axiom of Choice imposes sufficient structure on the system to solve the problem. Equivalent to the Axiom of Choice is Zorn’s Lemma, which is easier to understand. The lemma effectively states that the elements of any set can be uniquely labelled with real numbers. Thus, using real numbers as labels, there always exists a unique labelling of elements such that one element can be distinguished from the other.
The very reliance on an axiom, any axiom, violates FC, as no such a priori constructs are permissible in a First Class system. What is of interest with the Axiom of Choice is that it situates the way that mathematics resolves the distinguishing problem. Firstly, it has to resort to a construct at the axiom level. Secondly is equivalent to using an ad hoc labelling technology, a characteristic of all left side sciences. The Axiom of Choice, and its fundamental lemma, thus articulates quite clearly, the way not to proceed: Don’t use labels.
Structure
Structure is in the mind of the beholder. For the left side sciences the beholder is the impersonal subject providing the much sought after ‘mind independent’ point of view. This primary opposition between the impersonal subject and its object is ignored by left side science and replaced with an opposition of its own making, that of the rigid dichotomy between abstract theory and its object. In left side mathematics, the primary dichotomy becomes that between a set of axioms and a world of deductively explorable mathematical objects so predetermined, either explicitly or implicitly.
For right side science, the mind of the beholder is of primordial importance and is always present. Not only is the impersonal subject present, but also the personal. There are many ways of interpreting these two kinds of subject. As mentioned previously, the subject as placeholder and the subject as value is one possibility. A more mathematical flavour might be to call them the “covariant” and “contravariant” subjects, but one must be on guard not to slip into abstraction ways of thought. Both these two kinds of subject are simultaneously present in any whole considered by right side science, The science of wholes is the speciality of the right side of the epistemological brain. What matters is the generic subject formed by a highly primitive, primordial Clifford-Grassmann style “geometric product” of these two subjects (together with their respective worlds). The end result is a the generic subject in the form of a “quaternion” kind of Three-Plus-One structure, a semiotic square which can be more formally understood in terms of the ontological gender typing construct. In the right side science paradigm, this artifice occupies centre stage at all times. One could even say that it is centre stage.
One way of understanding the generic subject is to realise that it suffers from an incurable disease. The disease is called monism. Patients suffering from monism exhibit the pathological symptoms of being totally incapable of distinguishing the difference between the real world and their conception of it. Both appear to be the one and the same thing. Curiously, most human subjects, at least when not on hallucinogenic drugs or suffering from a deep schizophrenic episode, also seem to exhibit these symptoms .
Right side science not only must articulate the basic architecture of the generic subject but also of the generic objects. There are four types of generic object, four bases distinguished one from the other by binary gender typing. The typing of bases is determined relative to each other and ultimately compatible with the polarity conventions established by the subject, the ultimate arbitrator of type. These four bases can be represented by four binary gendered typed arrows. The problem now is to establish how these arrows can be combined to form elementary structures, without violating FC.
From a left side science perspective, if a right side science were at all possible it would present as some kind of meta science, metaphysics or meta mathematics equipped with its own metalanguage. Such a science is not possible under the ambit of left side paradigm dominated, as it must be, by its atomistic and dualistic worldview. However, even though fundamentally incompatible with FC, some accommodations can be made to achieve a kind of Partial First Classness (PFC). The resulting science will not be a true metaphysics but at least pass as a poor man’s cousin.
The Sad Story of Mereology
One such accommodation is the rather obscure quasi-mathematical discipline called mereology, a left side attempt at a science of wholes and parts. Mereology is an exercise in mathematical logic. It achieves PFC by removing the rigid set theoretic dichotomy between sets and the elements that they contain. This is achieved by ignoring any explicit reference to the elements of a set and only considering containment relations between sets. Sets do not contain elements, they contain other sets. Contained sets are parts of the containing set. Different axiomatic schemes are set up to formalise this kind of structure where wholes contain parts and PFC is achieved by both parts and wholes being sets.
Mereology is of interest because it is essentially an attempt to formalise has-a relations between entities. Such structure finds echoes in the class inheritance structure of Object Oriented programming systems, for example. There are also echoes with our initial development of right side science where the has-a relation is paramount. However, right side science grants comparable prominence to is-a relations. In fact, the basic building block involved the gender construct where the feminine ontological gender corresponds to the has-a relation and the corresponding masculine gender to the is-a relation. The core of right side science, with its ontological vocation, consists of the dialectic of the has-a and is-a relationship. In mereology the has-a relation is axiomatised in terms of some kind of partially ordered structure such as set inclusion. As for any ontological is-a structure, that is hard wired into the axioms. Being a left side science mereology does not entertain any kind of is-a has-a dialectic.
A. N. Whitehead, in his philosophical quest for a holistic rationalist science, extended mereology concepts to geometry and achieved a geometric PFC (Whitehead, 1919). In this case, the rigid dichotomy between geometric objects with extension and geometric objects with no extension (points) was avoided to produce a pointless geometry. A pointless geometry is a right side kind of geometry. However, the geometry was caste in a left side, abstract, dualistic, atomist framework. In the final count, the system inevitably violates FC on practically every other front. Nevertheless, mereology is worth mentioning here as it expresses many of the aspirations of right side science even though it fundamentally lacks the necessary equipment to deliver the goods. In this respect, the mereology-based paper “Steps Toward a Constructive Nominalism” (Goodman, et al., 1947) is notable. In espousing constructionism and nominalism, the paper articulates important hallmarks of right side science. In addition, the authors start the paper with the doctrinal declaration: “We do not believe in abstract entities. No one supposes that abstract entities—classes, relations, properties, etc.— exist in space-time; but we mean more than this. We renounce them altogether.” This rejection of abstraction is yet another fundamental tenant of right side science. However, declared within the confines of left side abstract axiomatic technology this anti-abstract belief becomes a bit of an oxymoron. It is like the Christmas turkey that struts into the kitchen valiantly declaring that it does not believe that turkeys are food.
From our perspective, mereology is interesting more for its aspirations than its achievements. What we want is a left side discipline that can properly formalise the very essence of mathematics and that comes from within mathematics itself. What we need is an abstract theory of abstract mathematics, and that naturally leads to Category Theory, the meta-mathematics of mathematics. It is with Category Theory that we can find a formal specification of the kind of structure that is anathema to our right side science. We will use Category Theory as a formal negative indication of what we are up against in trying to resolve the Kantian problem.
Category Theory Structure Violates FC
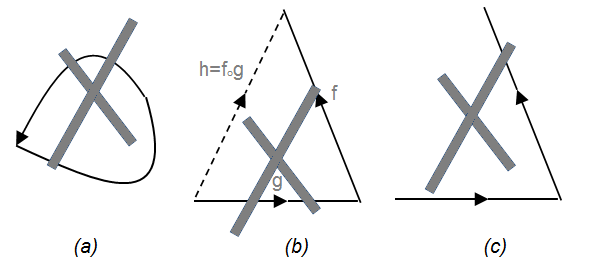
Category Theory provides abstract representations of mathematical structure in terms of a collection of objects and a collection arrows or morphisms between the objects. The specificity of mathematical structure is represented by the arrows and in no way by any explicit internal structure of the objects. The approach is thus structuralist in nature. Representation of the most elementary mathematical structure starts with placing two arrows end to end. This represents the composition of two arrows. Composition of arrows must satisfy two axioms, identity and associativity relying on the structures illustrated in Figure B 3 . Both of these structures violate FC.
Figure B 3(b) represents the composition of two arrows f and g to determine a third arrow h thus satisfying associativity. This violate FC because the arrow g is in an absolute ordering relationship with the arrow f. In a system satisfying FC, no entity can be absolutely before or after any other. Thus, even the two arrows shown in Figure B 3(c) is an FC violation. Thus not only is associativity prohibited but any kind of composition. We could call this disallowing of any absolute ordering relationships, the Parmenidean condition. For FC, the only thing that is must be immediate, not anterior, nor posterior.
A mathematical category requires the notion of composition identity defined for each object. This requires arrows that close back on themselves to form a loop as shown in Figure B 3(a). This structure also violates FC as it infers than the same entity can be different to itself. We will call it the Heraclitus principle expressed by the saying that “You can’t put your foot into the same river twice”. It is a special case of the Parmenidean condition. This prohibition is a subtle one but suffice to say that it can be represented by a prohibition on circular arrows.
Without getting into messy details, it suffices to say that the formal axiomatic mathematical Category abstractly states the minimal structural characteristics that a system must possess in order to qualify as mathematics. What interests us is not mathematics, but its opposite, anti-mathematics. We informally define anti-mathematics, as being everything that mathematics is not. At the abstract pinnacle of mathematics, we find Category Theory. The anti-mathematical counterpart will be the Anti-Category. The only thing in common between the Category and the Anti-Category will be that they both exploit an arrow theoretic methodology.in one way or another.
The Anti-Category and the Kantian Conditions
The conditions on the Anti-Category can be summed up as:
- Unlike the Category, the Anti-Category cannot be abstract. This can be achieved by prohibiting dualistic structures, the essence of abstraction.
- Thus, unlike the Category, the Anti-Category cannot tolerate a duality between a collection of objects and a collection of arrows. For the Anti-Category not to violate FC, the mantra is that all entities are arrows. In this way, any entity will possess extent. From an ontological point of view, we reiterate the Stoic mantra that only bodies exists. Point like entities do not exist.
- Unlike the Category, there can be no identity, no associativity and not even composition of arrows.
- There can be no axioms as any such predetermining structure violates FC.
We will call these conditions, the Kantian conditions for determining a formal structure that is totally devoid of any predetermining considerations. Realise an apparatus that satisfies the Kantian conditions and one has resolved the Kantian problem. In other words, one would have provided a formal basis for right sides science, the monistic counterpart of the dualistic left side sciences. Bot easy, but it can be done.
The axiomatic formalisation of mathematical categories is quite precise. Taking these conditions in the negative provides draconian requirements on the right side counterpart to the Category, the Anti-Category. Briefly, arrows determining anti-categories cannot form loops or be concatenated end to end. This leaves plenty of slack for finding a solution to the riddle. At least the Kantian problem is starting to look tractable.
Arrow Theoretic Methodology
Category Theory is based on an arrow theoretic methodology. It expresses its fundamentals in terms of arrow diagrams. Our task is to develop the right side counterpart of the Category in terms of the Anti-Category. If we can achieve this objective then we will have made a breakthrough is resolving the Kantian problem, the fundamental thrust of this paper. Thus, we claim that, in addition to the known left side arrow theoretic methodology of Category Theory, there must be a complementary right side arrow theoretic methodology. Our task is to bring this right side version of arrow theoretic methodology into the light of day. In the process, we will see that the traditional left side version specialises uniquely in the syntaxical aspects of structure and is virtually devoid of fundamental semantic considerations. On the right side of the equation, we will demonstrate that right side arrow theoretic structures are virtually syntax free, concentrating uniquely on semantics. One could say that traditional left side abstract approach to semantics leads to a syntax only account: Abstract semantics distils down to syntaxical expression. On the other hand, rhea right side paradigm approach to semantics leads to generic, non-abstract semantics. This kind of semantics is ultimately expressed in the gender calculus in the form of a syntax free generic code, a code capable of coding any semantics whatsoever that is compatible with FC.