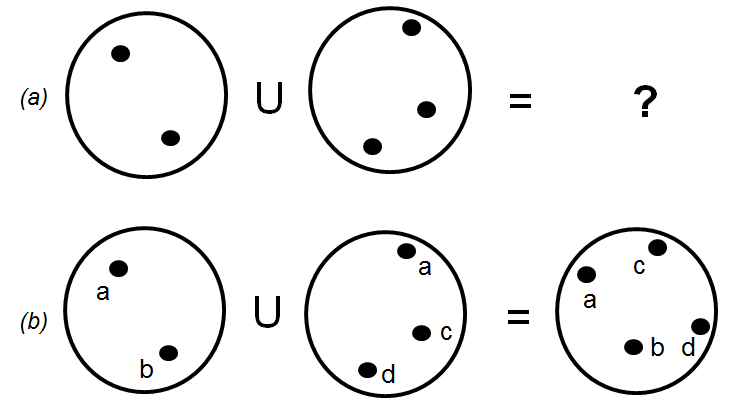The following snippet is about Category Theory. If there is anything likely to scare the troops, it’s Category Theory. A long while back I met a well-known Australian philosopher of the analytic tradition. He was into mereology and made his long career in this kind of area. Not many people have heard of mereology. You might have to try Google or look at my last post here. I don’t want to belittle mereology because after all Whitehead was quite involved with it, and he was no lightweight. Pity he spent so much time with Russell. No one is perfect. I asked the professor what he thought about Category Theory. He replied that he didn’t know anything about it except that it was hard. I was flabbergasted. I still am.
In the snippet, which follows, I describe a very first glimpse of Category Theory and its philosophical implications. Category Theory, whether you like it or not, sits at the top of formal axiomatic mathematics. In other words, it sits at the top of abstract science, as we customarily know it. It articulates the shape of abstract (Platonic) ideas in the form of (so-called) universal constructions (limits, colimits, pushouts, pullbacks, and equalisers for example). Who cares? Good question. These universal constructions are not actually universal but more in the line of being very general. There is an important difference between the universal and the general. The general applies to everything but not everywhere. The universal applies everywhere but not to everything. People confuse the two. Traditional sciences home in on the general. These sciences, including axiomatic mathematics, are based on generalisation, on abstraction. I call them left side sciences. The true universal is not abstract but generic. I call this right side science. Developing right side, truly universal science, is my project. Lucky for me, I am not the first. The Stoics, and in particular Chrysippus, appear to be the first, at least in the Western World.
It is a long story, much simpler than you think. If you have never really understood Category Theory, this thing that is important but “hard,” the following snippet might get us into the foothills. It might be worth the effort. Pleas keep in mind that our approach is not at all orthodox and might upset mathematicians.
In the final thrust of things, the difference between the general (Platonic) constructs of traditional left side science and the true (generic) universals of right side science is that the latter exist, and the former do not. Abstractions are useful but they don’t exist, as such.
The idea is to look at the “arrow theoretic” approach of Category Theory as a way of explaining things without words. You use arrows and diagrams instead. This works very well for deep abstract mathematical kinds of concepts. That is what Category Theory is about. For the abstract mathematician, this is as good as it gets. But is there another non-abstract way of explaining things with arrows? A generic way, for example.
—————————————————————————————
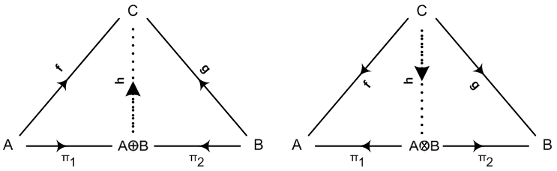
That is enough of the hyperbole; let us look now at the left side version of the arrow theoretic method. We start with a practical example from Category Theory. Figure B 4 shows the categorical representation of the categorical sum and the categorical product of objects in a Category. We won’t attempt to understand the diagrams for the moment. We simply note that the diagrams look quite neat and clean, quite beautiful in fact.
The notion of the product and sum is fundamental to mathematics and crops up in many guises. Already, the Categorical diagrams reveal something that can be difficult to describe otherwise: In general, product operations are a kind of dual of sum operations. This can be seen simply by reversing the direction of the arrows for the sum diagram to produce the dual diagram. This corresponds to the categorical product.
In order to get an understanding of the arrow theoretic methodology involved we will assume that the objects of the category are sets and that the sum of two sets will be set theoretic union and the product will be set intersection. Now consider the set theory problem illustrated in Figure B 5(a). The problem is to work out the set theoretic union of two sets without using labels. The answer is that it can’t be done. However, in Figure B 5(b), we have invoked the Axiom of Choice, which says that any set can be labelled. The elements of each of the two sets have thus been dutifully labelled and the corresponding result of set theoretic union is shown on the right, problem solved. Of course, if we had chosen a different labelling, we would get a different result. The conclusion here is that the ability to label is very important in Set Theory. That is why Set Theory cannot do without the Axiom of Choice.
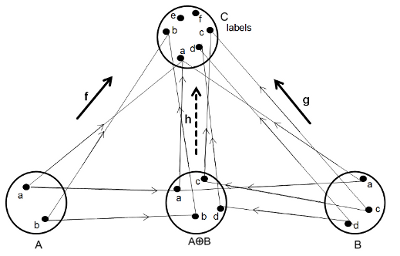
Let us now start moving towards a categorical approach to the problem and see how Category Theory can get by without any explicit labelling technology whatsoever. The labelling used in Figure B 5(b) was quite ad hoc. We now interpret this ad hoc labelling as a very nuts and bolts model of the Category Theory representation of categorical sum. Using this more elaborate labelling technology, the ad hoc labelling is replaced by a system of labelling as shown in Figure B 6. In this diagram, the set C consists of a large enough set of labels to do the job. The sets A, B and their sum are each labelled by bunches of connections between each of the sets and the labels in C. The three bunches of lightly drawn arrows are instances of the morphism arrows f, g, and h of the highly abstract categorical representation of sum shown in Figure B 4. The Category Theory represents all the possible indexing instances possible for determining the abstract mathematical notion of sum and does so at the most abstract level.
We will now look at the specificities of this kind of this left side arrow theoretic methodology. Our discussion is motivated by the quest for a sibling right side arrow theoretic methodology. Our aim is to resolve the Kantian problem and so the discussion has a philosophical and even a psychological tone. One of our objectives is to cure mathematics of the hemi-neglect syndrome mentioned in Part 1. Against blatant neglect, we must show that there is another way, another side to it all.
 |
| Figure B 6 |
Figure B6 The Category Theory diagram can be thought of as an abstraction of a labelling system. In Category Theory all this detail is superfluous and no explicit labelling is necessary..
Traditional Arrow Theoretic Methodology
Our immediate task is to characterise the left side arrow theoretic methodology of Category Theory. We will look at how Category Theory respects First Classness (FC), how and where it violates FC, and its overall architectural characteristics.
The first startling realisation is that Category Theory, right from the start, formally articulates the core requirement of FC notably that no entity be anterior to any other. What this means is that in any Category Theory diagram, no arrow can be said to be before or after any other arrow. There can be no concatenation of arrows. In other words, Category Theory starts off without any appeal to the composition of arrows. However, there are two caveats. Firstly, we must add the caveat that this FC only applies to the non-dotted arrows. The dotted arrow is added ‘to make the diagram commutes.’ The orientation and location of the dotted arrow is such that it always violates FC as it appeals to the fundamental structural mechanism of Category Theory, associativity and the composition of arrows.
There is a second caveat that we add in small print. This is to do with identity arrows, which clearly violated FC. In practice, this is the case anyway as identity arrows are usually only explicitly incorporated in the diagram when pertinent and that is usually after adding the dotted arrow, not before. We will sweep this aspect under the carpet by saying that, except for the identity arrows, the rest of the arrows in an arrows diagram, excluding the dotted arrow, all respect FC.
At this point, we will introduce some terminology for describing the two kinds of arrow in an arrow diagram. We will refer to the dotted arrow as being real and all the other arrows as being imaginary. Thus, every arrow diagram has an imaginary part and a real part. The real part consists of one single arrow, the specificity of which is represented by the geometric configuration of the arrows making up the imaginary part of the diagram. The imaginary arrows, relative to each other, respect FC. They all determine the specificity of the real arrow.
Arrow diagram of Category Theory is a technology for representing the specificity of a “real” entity, the entity represented by the dotted arrow added to the diagram in order to make it commute. All of the specificity is encoded in the topological configuration of the imaginary arrows relative to each other and to the real. There is no need for labels. In practice, mathematicians label the various arrows making up the imaginary part and real parts of the diagram, but this is only to make it easier to talk about the structure. The labels themselves impart no additional structural specificity to the diagram.